
3.已知命題p、q,“非p為真命題”是“p或q是假命題”的 ( )
A.充分而不必要條件 B.必要而不充分條件
C.充要條件 D.既不充分也不必要條件
2.與函數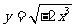 有相同圖象的一個函數是 ( )
有相同圖象的一個函數是 ( )
A.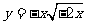 B.
B.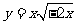
C.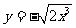 D.
D.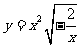
1.若集合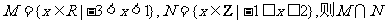 = ( )
= ( )
A.{0} B.{-1,0} C.{-1,0,1} D.{-2,-1,0,1,2}
指數形式的函數定義域、值域的求法,判斷其單調性和奇偶性的方法
求下列函數的定義域和值域:
⑴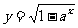 ⑵
⑵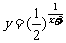
解:⑴要使函數有意義,必須
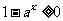 ,
, 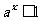
當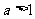 時
時 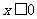 ; 當
; 當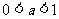 時
時 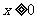
∵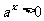 ∴
∴ ∴值域為
∴值域為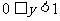
⑵要使函數有意義,必須 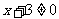 即
即 
∵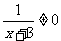 ∴
∴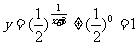
又∵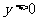 ∴值域為
∴值域為 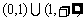
例1求下列函數的定義域、值域:
⑴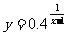 ⑵
⑵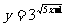 ⑶
⑶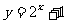

分析:此題要利用指數函數的定義域、值域,并結合指數函數的圖象 注意向學生指出函數的定義域就是使函數表達式有意義的自變量x的取值范圍
注意向學生指出函數的定義域就是使函數表達式有意義的自變量x的取值范圍
解(1)由x-1≠0得x≠1
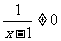 所以,所求函數定義域為{x|x≠1}
所以,所求函數定義域為{x|x≠1}
由
,得y≠1
所以,所求函數值域為{y|y>0且y≠1}
說明:對于值域的求解,在向學生解釋時,可以令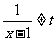 ,考察指數函數y=
,考察指數函數y=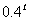 ,并結合圖象直觀地得到,以下兩題可作類似處理
,并結合圖象直觀地得到,以下兩題可作類似處理
(2)由5x-1≥0得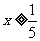

所以,所求函數定義域為{x|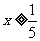 }
}
由 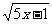 ≥0得y≥1
≥0得y≥1
所以,所求函數值域為{y|y≥1}
(3)所求函數定義域為R
由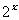 >0可得
>0可得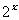 +1>1
+1>1
所以,所求函數值域為{y|y>1}
通過此例題的訓練,學會利用指數函數的定義域、值域去求解指數形式的復合函數的定義域、值域,還應注意書寫步驟與格式的規范性
例2求函數 的單調區間,并證明
的單調區間,并證明
解:設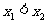
則
∵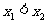 ∴
∴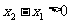
當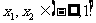 時,
時,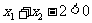 這時
這時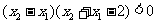
即 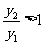 ∴
∴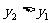 ,函數單調遞增
,函數單調遞增
當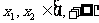 時,
時, 這時
這時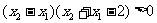
即 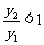 ∴
∴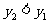 ,函數單調遞減
,函數單調遞減
∴函數y在 上單調遞增,在
上單調遞增,在 上單調遞減
上單調遞減
解法二、(用復合函數的單調性):
設: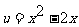 則:
則: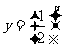
對任意的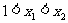 ,有
,有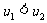 ,又∵
,又∵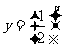 是減函數
是減函數
∴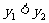 ∴
∴ 在
在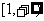 是減函數
是減函數
對任意的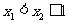 ,有
,有 ,又∵
,又∵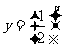 是減函數
是減函數
∴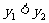 ∴
∴ 在
在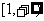 是增函數
是增函數
引申:求函數 的值域 (
的值域 (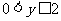 )
)
小結:復合函數單調性的判斷(見第8課時)
例3設a是實數,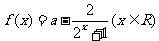
試證明對于任意a,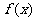 為增函數;
為增函數;
分析:此題雖形式較為復雜,但應嚴格按照單調性、奇偶性的定義進行證明 還應要求學生注意不同題型的解答方法
還應要求學生注意不同題型的解答方法
(1)證明:設 ∈R,且
∈R,且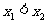
則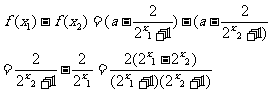

由于指數函數
y=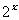 在R上是增函數,且
在R上是增函數,且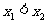 ,
,
所以
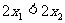 即
即
 <0,
<0,
又由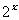 >0得
>0得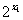 +1>0,
+1>0,  +1>0
+1>0
所以 <0即
<0即
因為此結論與a取值無關,所以對于a取任意實數,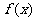 為增函數
為增函數
評述:上述證明過程中,在對差式正負判斷時,利用了指數函數的值域及單調性
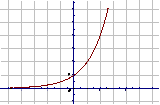
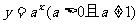 的圖象和性質
的圖象和性質
|
|
a>1 |
0<a<1 |
|
圖 象 |
 |
 |
|
性 質 |
(1)定義域:R |
|
|
(2)值域:(0,+∞) |
||
|
(3)過點(0,1),即x=0時,y=1 |
||
|
(4)在 R上是增函數 |
(4)在R上是減函數 |
22.(本小題滿分14分)
已知函數f(x)的定義域為(0,+∞),且對任意的正實數x,y都有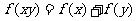 ,且當x>1時,f(x)>0,f(4)=1.
,且當x>1時,f(x)>0,f(4)=1.
(1) 求證:f(1)=0;
(2)
求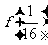 ;
;
(3) 求證:f(x)在(0,+∞)上為增函數;
(4)
解不等式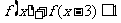 .
.
21.(本小題滿分12分)
已知二次函數g(x)的圖象經過坐標原點,且滿足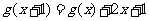 。設函數
。設函數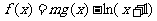 ,其中m為非零常數.
,其中m為非零常數.
(1)求函數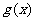 的解析式;
的解析式;
(2)當-2<m<0時,判斷函數f(x)的單調性并且說明理由;
(3)證明:對任意的正整數n,不等式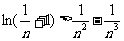 恒成立.
恒成立.
20.(本小題滿分12分)
已知函數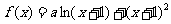 在x=1處有極值.
在x=1處有極值.
(1) 求實數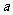 的值;
的值;
(2) 求函數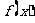 的單調區間;
的單調區間;
(3) 令g(x)=  ,若曲線g(x)在(1,g(1))處的切線與兩坐標軸分別交于A、B兩點(
,若曲線g(x)在(1,g(1))處的切線與兩坐標軸分別交于A、B兩點(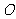 為坐標原點),求
為坐標原點),求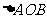 的面積.
的面積.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com