例1求下列函數的定義域.值域: ⑴ ⑵ ⑶ 分析:此題要利用指數函數的定義域.值域.并結合指數函數的圖象注意向學生指出函數的定義域就是使函數表達式有意義的自變量x的取值范圍 解(1)由x-1≠0得x≠1 所以.所求函數定義域為{x|x≠1} 由 .得y≠1 所以.所求函數值域為{y|y>0且y≠1} 說明:對于值域的求解.在向學生解釋時.可以令.考察指數函數y=,并結合圖象直觀地得到.以下兩題可作類似處理 (2)由5x-1≥0得 所以.所求函數定義域為{x|} 由 ≥0得y≥1 所以.所求函數值域為{y|y≥1} (3)所求函數定義域為R 由>0可得+1>1 所以.所求函數值域為{y|y>1} 通過此例題的訓練.學會利用指數函數的定義域.值域去求解指數形式的復合函數的定義域.值域.還應注意書寫步驟與格式的規范性 例2求函數的單調區間.并證明 解:設 則 ∵ ∴ 當時. 這時 即 ∴.函數單調遞增 當時. 這時 即 ∴.函數單調遞減 ∴函數y在上單調遞增.在上單調遞減 解法二.: 設: 則: 對任意的.有.又∵是減函數 ∴ ∴在是減函數 對任意的.有.又∵是減函數 ∴ ∴在是增函數 引申:求函數的值域 () 小結:復合函數單調性的判斷 例3設a是實數. 試證明對于任意a,為增函數, 分析:此題雖形式較為復雜.但應嚴格按照單調性.奇偶性的定義進行證明還應要求學生注意不同題型的解答方法 (1)證明:設∈R,且 則 由于指數函數 y=在R上是增函數,且, 所以即<0. 又由>0得+1>0, +1>0 所以<0即 因為此結論與a取值無關.所以對于a取任意實數.為增函數 評述:上述證明過程中.在對差式正負判斷時.利用了指數函數的值域及單調性 【
查看更多】
題目列表(包括答案和解析)
例2.設f(x)是定義在[-3,
]上的函數,求下列函數的定義域(1)
y=f(-2)(2)
y=f()(a≠0)
查看答案和解析>>
例2.設f(x)是定義在[-3,
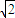
]上的函數,求下列函數的定義域(1)

(2)
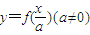
查看答案和解析>>
主站蜘蛛池模板:
日韩精品播放
|
亚洲在线免费观看
|
亚洲精品乱码久久久久久
|
久久亚洲一区二区
|
最新午夜综合福利视频
|
岛国伊人
|
国产日韩欧美在线观看
|
久草电影在线
|
久久三区
|
国产精品久久久久一区二区三区
|
日韩欧美视频一区
|
91日日|
琪琪午夜伦伦电影福利片
|
国产一区二区三区精品久久久
|
色视频网站免费看
|
日本久久99
|
亚洲视频综合
|
欧美久久久久久
|
yy6080久久伦理一区二区
|
国产精品久久
|
成人精品一二三区
|
欧美日韩精品一区二区
|
日韩在线观看一区二区三区
|
黄av在线
|
91精品久久久久久久久久
|
久久久久久久久久久久网站
|
国产精品久久久久aaaa九色
|
亚洲一区二区三区四区在线观看
|
国产精品美乳一区二区免费
|
精品黑人一区二区三区久久
|
欧美久久久久久久久久伊人
|
欧美成人一区二区三区片免费
|
一级欧美一级日韩片
|
国产成人在线播放
|
色本道|
欧美一区二区三区成人精品
|
娇小12—13毛片
|
日韩av一区在线观看
|
成人伊人网
|
亚洲欧美一区二区三区在线
|
国产综合亚洲精品一区二
|

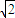 ]上的函數,求下列函數的定義域(1)
]上的函數,求下列函數的定義域(1) (2)
(2)