
(1)設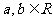 ,則
,則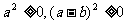 (當且僅當
時取等號)
(當且僅當
時取等號)
(2) (當且僅當
時取等號);
(當且僅當
時取等號); (當且僅當
時取等號)
(當且僅當
時取等號)
(3)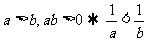 ;
;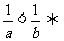 ;
;
注意:上述等號“=”成立的條件;
若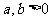 ,則
,則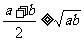 (當且僅當
(當且僅當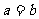 時取等號)
時取等號)
基本變形:① ;
;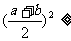 ;
;
②若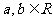 ,則
,則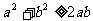 ,
,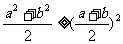
基本應用:①放縮,變形;
②求函數最值:注意:①一正二定三取等;②積定和小,和定積大。
當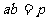 (常數),當且僅當
時,
;
(常數),當且僅當
時,
;
當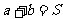 (常數),當且僅當
時,
;
(常數),當且僅當
時,
;
常用的方法為:拆、湊、平方;
如:①函數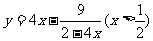 的最小值
。
的最小值
。
②若正數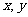 滿足
滿足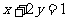 ,則
,則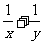 的最小值
。
的最小值
。
(1)一元一次不等式:
Ⅰ、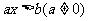 :⑴若
:⑴若 ,則
;⑵若
,則
;⑵若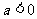 ,則
;
,則
;
Ⅱ、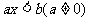 :⑴若
:⑴若 ,則
;⑵若
,則
;⑵若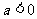 ,則
;
,則
;
(2)一元二次不等式: 一元二次不等式二次項系數小于零的,同解變形為二次項系數大于零;注:要對 進行討論:
進行討論:
(5)絕對值不等式:若 ,則
,則 ;
;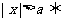 ;
;
注意:(1).幾何意義: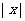 :
;
:
;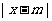 :
;
:
;
(2)解有關絕對值的問題,考慮去絕對值,去絕對值的方法有:
⑴對絕對值內的部分按大于、等于、小于零進行討論去絕對值;①若 則
則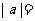 ;②若
;②若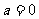 則
則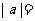 ;③若
;③若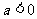 則
則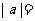 ;
;
(3).通過兩邊平方去絕對值;需要注意的是不等號兩邊為非負值。
(4).含有多個絕對值符號的不等式可用“按零點分區間討論”的方法來解。
(6)分式不等式的解法:通解變形為整式不等式;
⑴ ;⑵
;⑵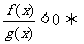 ;
;
⑶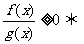 ;⑷
;⑷ ;
;
(7)不等式組的解法:分別求出不等式組中,每個不等式的解集,然后求其交集,即是這個不等式組的解集,在求交集中,通常把每個不等式的解集畫在同一條數軸上,取它們的公共部分。
(8)解含有參數的不等式:
12.(07北京15)記關于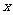 的不等式
的不等式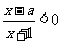 的解集為
的解集為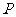 ,不等式
,不等式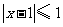 的解集為
的解集為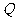 .(I)若
.(I)若 ,求
,求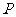 ;(II)若
;(II)若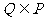 ,求正數
,求正數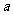 的取值范圍.
的取值范圍.
11.(07全國1)設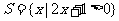 ,
,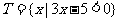 ,則
,則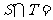
10.(07江蘇6)設函數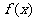 定義在實數集上,它的圖像關于直線
定義在實數集上,它的圖像關于直線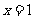 對稱,且當
對稱,且當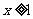 時,
時,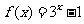 ,則有
,則有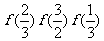 的大小關系
的大小關系
9.(07安徽理5)若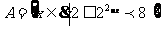 ,
,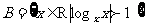 ,則
,則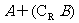 的元素個數為 .
的元素個數為 .
8.(07安徽)若對任意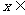 R,不等式
R,不等式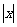 ≥ax恒成立,則實數a的取值范圍是
≥ax恒成立,則實數a的取值范圍是
7.(07山東理)函數y=loga(x+3)-1(a>0,a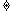 1)的圖象恒過定點A,若點A在直線mx+ny+1=0上,其中mn>0,則
1)的圖象恒過定點A,若點A在直線mx+ny+1=0上,其中mn>0,則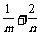 的最小值為
.
的最小值為
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com