
2.兩個平面垂直的判定方法(判定方法有兩種,一是利用定義,二是利用判定定理.)
1.兩個平面垂直的定義、畫法
3.如圖,正方體的棱長為1,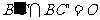 ,求:
,求:
(1)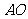 與
與 所成角;
所成角;
(2)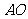 與平面
與平面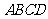 所成角的正切值;
所成角的正切值;
(3)平面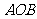 與平面
與平面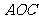 所成角
所成角
解:(1)∵ ∴
∴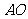 與
與 所成角就是
所成角就是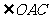
∵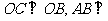 平面
平面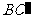 ∴
∴ (三垂線定理)
(三垂線定理)
在 中,
中,  ∴
∴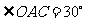
(2)作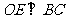 ,平面
,平面 平面
平面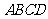
∴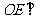 平面
平面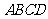 ,
,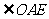 為
為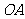 與平面
與平面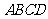 所成角
所成角
在 中,
中,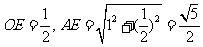 ∴
∴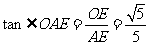
(3)∵ ∴
∴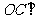 平面
平面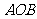
又∵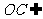 平面
平面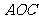 ∴平面
∴平面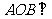 平面
平面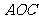
即平面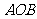 與平面
與平面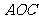 所成角為
所成角為

說明:本題包含了線線角,線面角和面面角三類問題,求角度問題主要是求兩條異面直線所成角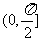 ,直線和平面所成角
,直線和平面所成角 ,二面角
,二面角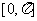 三種;求角度問題解題的一般步驟是:(1)找出這個角;(2)證明該角符合題意;(3)作出這個角所在的三角形,解三角形,求出角;求角度問題不論哪種情況都歸結到兩條直線所成角問題,即在線線成角中找到答案
三種;求角度問題解題的一般步驟是:(1)找出這個角;(2)證明該角符合題意;(3)作出這個角所在的三角形,解三角形,求出角;求角度問題不論哪種情況都歸結到兩條直線所成角問題,即在線線成角中找到答案
2.如果二面角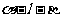 的平面角是銳角,點
的平面角是銳角,點 到
到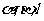 的距離分別為
的距離分別為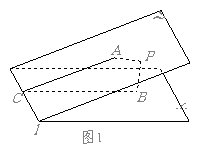
 ,求二面角的大小
,求二面角的大小
分析:點 可能在二面角
可能在二面角 內部,也可能在外部,應區別處理
內部,也可能在外部,應區別處理
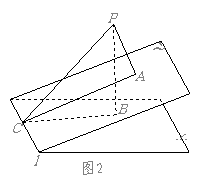
解:如圖1是點 在二面角
在二面角 的內部時,圖2是點
的內部時,圖2是點 在二面角
在二面角 外部時,
外部時,
 ∵
∵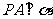 ∴
∴
∵ ∴面
∴面
同理,面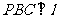
而面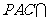 面
面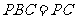
∴面 與面
與面 應重合
應重合
即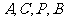 在同一平面內,
在同一平面內,
則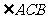 是二面角
是二面角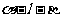 的平面角
的平面角
在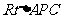 中,
中, ∴
∴
在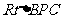 中,
中,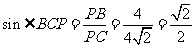 ∴
∴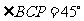
故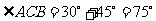 (圖1)或
(圖1)或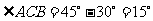 (圖2)
(圖2)
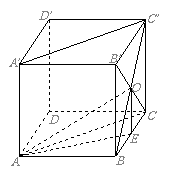 即二面角
即二面角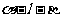 的大小為
的大小為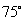 或
或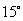

說明:作一個垂直于棱的平面,此平面與兩個半平面的交線所成的角就是二面角的平面角
1.直角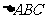 的斜邊
的斜邊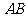 在平面
在平面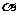 內,
內,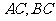 與
與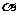 所成角分別為
所成角分別為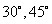 ,
, 是斜邊
是斜邊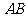 上的高線,求
上的高線,求 與平面
與平面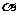 所成角的正弦值
所成角的正弦值
解:過點 作
作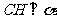 于點
于點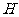 ,連接
,連接 ,
,
則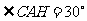 ,
,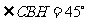 ,
,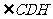 為所求
為所求 與
與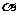 所成角,記為
所成角,記為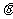 ,
,
 令
令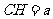 ,則
,則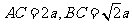 ,
,
則在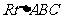 中,有
中,有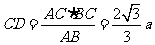
在 中,
中,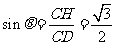
∴ 與平面
與平面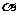 所成角的正弦值
所成角的正弦值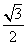 .
.
 例1
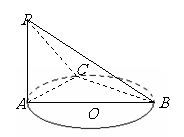
例1  如圖,已知
如圖,已知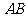 是圓
是圓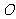 的直徑,
的直徑,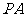 垂直于
垂直于 所在的平面,
所在的平面, 是圓周上不同于
是圓周上不同于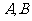 的任一點,求證:平面
的任一點,求證:平面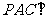 平面
平面 .
.
分析:根據“面面垂直”的判定定理,要證明兩平面互相垂直,只要在其中一個平面中尋找一條與另一平面垂直的直線即可
解:∵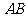 是圓
是圓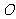 的直徑,∴
的直徑,∴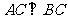 ,
,
又∵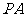 垂直于
垂直于 所在的平面,∴
所在的平面,∴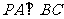 ,
,
∴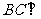 平面
平面 ,又
,又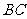 在平面
在平面 中,
中,
所以,平面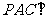 平面
平面 .
.
說明:由于平面 與平面
與平面 相交于
相交于 ,所以如果平面
,所以如果平面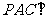 平面
平面 ,則在平面
,則在平面 中,垂直于
中,垂直于 的直線一定垂直于平面
的直線一定垂直于平面 ,這是尋找兩個平面的垂線的常用方法
,這是尋找兩個平面的垂線的常用方法
例2.已知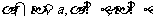 ,求證:
,求證: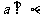 .
.
證明:設 ,
,
 在
在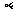 內取點
內取點 ,過
,過 作
作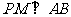 于
于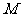 ,
,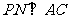 于點
于點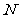 ,
,
∵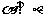 ,∴
,∴ ,
,
又∵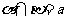 ,
,
∴ ,同理可得
,同理可得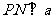 ,
,
∴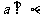 .
.
 例3.已知在一個
例3.已知在一個 的二面角的棱長有兩點
的二面角的棱長有兩點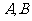 ,
, 分別是在這個二面角的兩個平面內,且垂直于線段
分別是在這個二面角的兩個平面內,且垂直于線段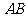 ,又知
,又知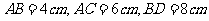 ,求
,求 的長
的長
解:由已知
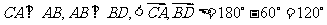 ,
,
∴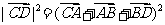
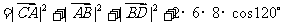
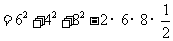
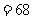 ,
,
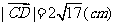
3.兩平面垂直的性質定理: 若兩個平面互相垂直,那么在一個平面內垂直于它們的交線的直線垂直于另一個平面
已知: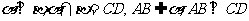 于點
于點 ,
,
求證: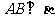 .(面面垂直
.(面面垂直 線面垂直)
線面垂直)
證明:在 內過
內過 作
作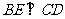 ,則由題意得
,則由題意得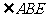 是
是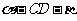 的平面角,
的平面角,
∵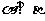 知
知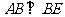 ,又∵
,又∵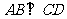 , ∴
, ∴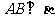 .
.
1  兩個平面垂直的定義:
兩個平面垂直的定義:
兩個相交成直二面角的兩個平面互相垂直;相交成直二面角的兩個平面叫做互相垂直的平面
2.兩平面垂直的判定定理: 如果一個平面經過另一個平面的一條垂線,那么這兩個平面互相垂直
 已知:直線
已知:直線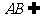 平面
平面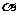 ,
,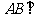 平面
平面 ,垂足為
,垂足為 ,
,
求證: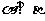 .(線面垂直
.(線面垂直 面面垂直)
面面垂直)
證明:如圖所示,令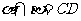 ,則
,則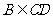 ,
,
 在
在 內過
內過 作
作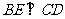 ,
,
∵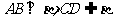 ,∴
,∴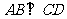 ,
,
∴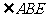 是二面角
是二面角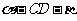 的平面角,
的平面角,
又∵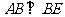 ,∴
,∴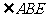 是直角,
是直角,
所以,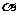 與
與 所成的二面角是直角,即
所成的二面角是直角,即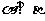 .
.
實例:建筑工地在砌墻時,常用鉛垂的線來檢查所砌的墻是否和水平面垂直
4.二面角的平面角:
(1)過二面角的棱上的一點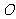 分別在兩個半平面內作棱的兩條垂線
分別在兩個半平面內作棱的兩條垂線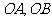 ,則
,則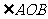 叫做二面角
叫做二面角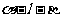 的平面角
的平面角
(2)一個平面垂直于二面角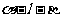 的棱
的棱 ,且與兩半平面交線分別為
,且與兩半平面交線分別為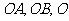 為垂足,則
為垂足,則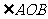 也是
也是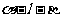 的平面角
的平面角
說明:(1)二面角的平面角范圍是 ;
;
(2)二面角的平面角為直角時,則稱為直二面角,組成直二面角的兩個平面互相垂直
2. 公式:已知平面a的斜線a與a內一直線b相交成θ角,且a與a相交成j1角,a在a上的射影c與b相交成j2角,則有
公式:已知平面a的斜線a與a內一直線b相交成θ角,且a與a相交成j1角,a在a上的射影c與b相交成j2角,則有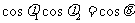
3  二面角的概念:平面內的一條直線把平面分為兩個部分,其中的每一部分叫做半平面;從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫做二面角的棱,每個半平面叫做二面角的面
二面角的概念:平面內的一條直線把平面分為兩個部分,其中的每一部分叫做半平面;從一條直線出發的兩個半平面所組成的圖形叫做二面角,這條直線叫做二面角的棱,每個半平面叫做二面角的面 若棱為
若棱為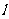 ,兩個面分別為
,兩個面分別為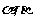 的二面角記為
的二面角記為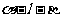 ;二面角的圖形表示:
;二面角的圖形表示:
第一種是臥式法,也稱為平臥式:
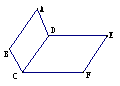
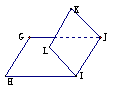
第二種是立式法,也稱為直立式:
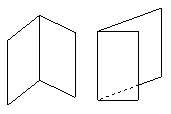

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com