
2.不共面的四個定點到平面 的距離都相等,這樣的平面
的距離都相等,這樣的平面 共有 (
D )
共有 (
D )
A.3個 B.4個 C.6個 D.7個
1.在棱長為a的正方體ABCD-A1B1C1D1中,與BC成異面直線且距離等于a的棱有( )
A.3條 B.4條 C.6條 D.7條
12.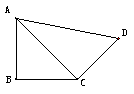 在平面四邊形ABCD中,已知AB=BC=CD=a,
在平面四邊形ABCD中,已知AB=BC=CD=a,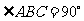 ,
,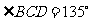 ,沿AC將四邊形折成直二面角B-AC-D,
,沿AC將四邊形折成直二面角B-AC-D,
(1)求證:面ABC⊥面BCD;
(2)求面ABD與面ACD所成的角。
解:(1)∵AB=BC,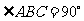 ,
,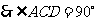 ,即AC⊥CD,
,即AC⊥CD,
又面ABC⊥面ACD,交線為AC,∴CD⊥面ABC,∴面ABC⊥面BCD。
(2)過B作BE⊥AC于E,過E作EF⊥AD于F,
∵面ABC⊥面ACD,AC為交線,
又∵BE⊥AC,∴BE⊥面ACD,∴EF為BF在平面ACD內的射影,
又∵EF⊥AD,∴AD⊥BF,∴∠BFE為二面角B-AD-C的平面角。
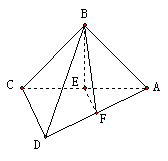 ∵AB=BC,BE⊥AC,∴E是AC的中點,∴
∵AB=BC,BE⊥AC,∴E是AC的中點,∴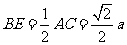 ,
,
又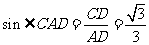 ,
,
∴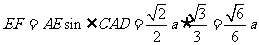 ,
,
 ,
,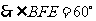 即為所求。
即為所求。
考查異面直線所成的角、直線與平面所成的角、平面與平面所成的二面角.要求掌握斜線在平面上的射影、直線與平面所成的角、二面角、二面角的平面角
理清求空間的角方法:一般是化歸為求兩條相交直線的夾角.通常應用“線線角抓平移,線面角抓射影,面面角抓平面角”而達到化歸目的.注意空間的角的計算應由“作、證、算”三個部分組成.首先應作出必要的輔助平面或輔助線;然后通過推理、論證找到某角就是所求的角;最后才是計算.
對于折疊問題, 要注意線的長度、角的大小及線線關系的變與不變。
11.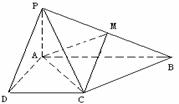 已知四棱錐P-ABCD的底面為直角梯形,AB∥DC,
已知四棱錐P-ABCD的底面為直角梯形,AB∥DC,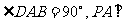 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=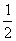 AB=1,M是PB的中點。
AB=1,M是PB的中點。
(1)求AC與PB所成的角;
(2)求面AMC與面BMC所成二面角的大小。
解:(1)過點B作BE//CA,且BE=CA,則
∠PBE是AC與PB所成的角.
連結AE,可知AC=CB=BE=AE=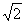 ,又AB=2,所以四邊形ACBE為正方形.
,又AB=2,所以四邊形ACBE為正方形.
由PA⊥面ABCD得∠PEB=90°,在Rt△PEB中BE=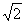 ,PB=
,PB=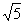 ,
,
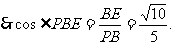

(2)作AN⊥CM,垂足為N,連結BN.在Rt△PAB中,AM=MB,
又AC=CB,∴△AMC≌△BMC,∴BN⊥CM,
故∠ANB為所求二面角的平面角.
∵CB⊥AC,由三垂線定理,得CB⊥PC,在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=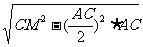 ,
,
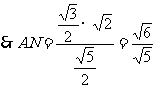 .
.
∴AB=2,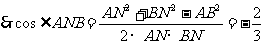 ,
,
故所求的二面角為
10.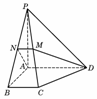 如圖,在四棱錐P-ABCD中,底面為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分別為PC、PB的中點.
如圖,在四棱錐P-ABCD中,底面為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分別為PC、PB的中點.
(1)求證:PB⊥DM;
(2)求CD與平面ADMN所成的角
解:(1)因為 是
是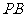 的中點,
的中點,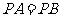 ,所以
,所以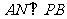 .
.
因為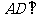 平面
平面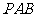 ,所以
,所以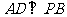 ,從而
,從而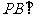 平面
平面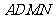 .
.
因為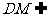 平面
平面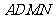 ,所以
,所以 .
.
(2)取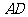 的中點
的中點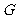 ,連結
,連結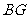 、
、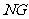 ,則
,則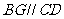 ,
,
所以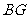 與平面
與平面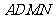 所成的角和
所成的角和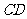 與平面
與平面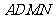 所成的角相等.
所成的角相等.
因為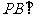 平面
平面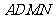 ,所以
,所以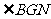 是
是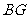 與平面
與平面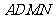 所成的角.
所成的角.
在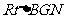 中,
中,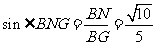 .
.
故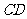 與平面
與平面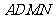 所成的角是
所成的角是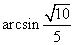 .
.
9.在正四棱錐P-ABCD中,若側面與底面所成二面角的大小為60°,則異面直線PA與BC所成角的大小等于_____________.(結果用反三角函數值表示)arctan2
8.四面體ABCD中,E、F分別是AC、BD的中點,若CD=2AB=2,EF⊥AB,則EF與CD所成的角等于_____________.30°
7.已知二面角 的大小為
的大小為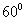 ,
,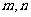 為異面直線,且
為異面直線,且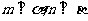 ,則
,則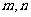 所成的角為
( B
)
所成的角為
( B
)
A.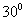 B.
B.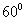 C.
C.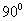 D.
D.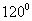
6.二面角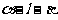 內有一點P,若P到平面
內有一點P,若P到平面 的距離分別是5,8,且P在平面
的距離分別是5,8,且P在平面 的內的射影間的距離為7,則二面角
的內的射影間的距離為7,則二面角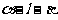 的度數是
( C
)
的度數是
( C
)
A.300 B.600 C.1200 D.1500
5.如圖,平面α⊥平面β,A∈α,B∈β,AB與兩平面α、β所成的角分別為和,過A、B分別作兩平面交線的垂線,垂足為A′、B′,則AB∶A′B′= ( A )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com