日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

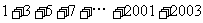　　 例1. 計算　　　　　 　　 解：設

　　 再把S倒過來寫：

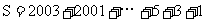
　　 相加得：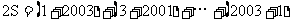　　

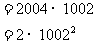
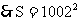
　　 列代數式時，有時需將題中的字母代入公式，這就要求正確進行代換。如圖，寫出圖中陰影部分面積的代數式為ab-(a-2x)(b-2x)。其中a與b分別表示長方形的長和寬，(a-2x)與(b-2x)分別表示小空白長方形的長和寬。▲

　　 列代數時要按要求規范地書寫。像數字與字母、字母與字母相乘可省略乘號不寫，數與數相乘必須寫乘號；除法可寫成分數形式，帶 分數與字母相乘需把代分數化為假分數，書寫單位名稱什么時不加括號，什么時要加括號。注意代數式括號的適當運用。

　　 列代數式時，一般應在語言敘述的數量關系中，先讀的先寫，如a的2倍與b的3倍的差，為2a-3b，不同級運算的語言，且又要體現出先低級運算，要把代數式中代表低級運算的這部分括起來，如a與b的差的3倍，為3(a-b)。

　　 要正確列代數式，只有分清數量之間的關系。如比m大3的數應為m+3；比一個數大3的數是m，則這個數為m-3；一個數是a的3位，這個數為3a；a是這個數的3倍，這個數為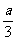。不要見多就加，見小就減，見倍就乘。

　　 列代數式時，要先認真審題，抓住關鍵詞語，仔細辯析詞義。如“除”與“除以”，“平方的差(或平方差)”與“差的平方”的詞義區分。例：“3除a”，“被3除得a”，“a與b兩數的平方差”，“a與b兩數差的平方”，分別為“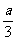”、“　 3a”、a²-b²、(a-b)²。

　　 例13. 已知拋物線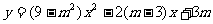的頂點D在雙曲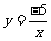線上，直線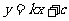經過點D和點C(a、b)且使y隨x的增大而減小，a、b滿足方程組，求這條直線的解析式。

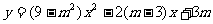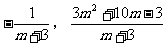　　 解：由拋物線的頂點D()在雙曲線上，可求得拋物線的解析式為：

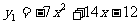　　 ，頂點D₁(1，－5)及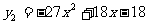

　　 頂點D₂(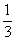，－15)

　　 解方程組得，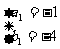

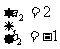
　　 即C₁(－1，－4)，C₂(2，－1)

　　 由題意知C點就是C₁(－1，－4)，所以過C₁、D₁的直線是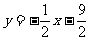；過C₁、D₂的直線是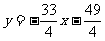

　　 例12. 若方程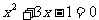的兩根分別為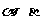，求經過點P(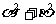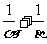，)和Q(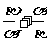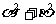，)的一次函數圖像的解析式

　　 解：由根與系數的關系得，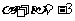

　　 ，

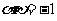
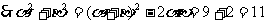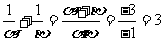
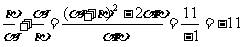
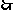　　 點P(11，3)、Q(－11，11)

　　 設過點P、Q的一次函數的解析式為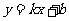

　　 則有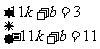

　　 解得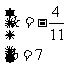

　　 故這個一次函數的解析式為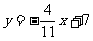

　　 例11. 如圖，在平面直角坐標系中，A、B是x軸上的兩點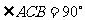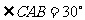，，，以AO、BO為直徑的半圓分別交AC、BC于E、F兩點，若C點的坐標為(0，3)。(1)求圖像過A、B、C三點的二次函數的解析式，并求其對稱軸；(2)求圖像過點E、F的一次函數的解析式。

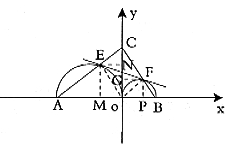
　　 解：(1)由直角三角形的知識易得點A(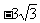，0)、B(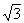，0)，由待定系數法可求得二次函數解析式為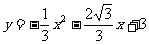，對稱軸是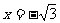

　　 (2)連結OE、OF，則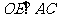、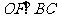。過E、F分別作x、y軸的垂線，垂足為M、N、P、G，易求得E(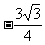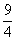，)、F(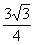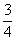，)由待定系數法可求得一次函數解析式為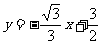

　　 例10. 已知函數的圖像過點A(1，4)，B(2，2)兩點，請寫出滿足上述條件的兩個不同的函數解析式，并簡要說明解答過程。

　　 解：(1)若經過A、B兩點的函數圖像是直線，由兩點式易得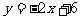

　　 (2)由于A、B兩點的橫、縱坐標的積都等于4，所以經過A、B兩點的函數圖像還可以是雙曲線，解析式為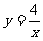

　　 (3)其它(略)