
5.說明:設數列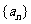 是等差數列,且公差為
是等差數列,且公差為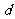 ,(Ⅰ)若項數為偶數,設共有
,(Ⅰ)若項數為偶數,設共有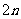 項,則①
項,則①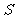 奇
奇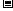
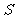 偶
偶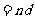 ; ②
; ② 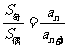 ;(Ⅱ)若項數為奇數,設共有
;(Ⅱ)若項數為奇數,設共有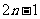 項,則①
項,則①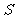 偶
偶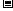
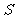 奇
奇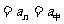 ;②
;②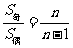 。
。
3.等差數列的性質:
(1)在等差數列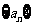 中,從第2項起,每一項是它相鄰二項的等差中項;
中,從第2項起,每一項是它相鄰二項的等差中項;
(2)在等差數列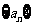 中,相隔等距離的項組成的數列是
中,相隔等距離的項組成的數列是 , 如:
, 如: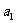 ,
, ,
, ,
,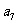 ,……;
,……; ,
,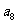 ,
,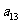 ,
,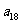 ,……;
,……;
(3)在等差數列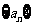 中,對任意
中,對任意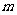 ,
,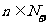 ,
,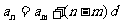 ,
,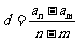
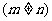 ;
;
(4)在等差數列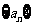 中,若
中,若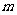 ,
,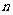 ,
, ,
,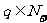 且
且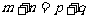 ,則
,則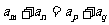 ;
;
2.等差數列的知識要點:
(1)等差數列定義an+1-an=d(常數)(n 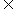 N),這是證明一個數列是等差數列的依據,要防止僅由前若干項,如a3-a2=a2-a1=d(常數)就說{an}是等差數列這樣的錯誤,判斷一個數列是否是等差數列。還可由an+an+2=2 an+1 即an+2-an+1=an+1-an 來判斷。
N),這是證明一個數列是等差數列的依據,要防止僅由前若干項,如a3-a2=a2-a1=d(常數)就說{an}是等差數列這樣的錯誤,判斷一個數列是否是等差數列。還可由an+an+2=2 an+1 即an+2-an+1=an+1-an 來判斷。
(2)等差數列的通項為an=a1+(n-1)d.可整理成an=an+(a1-d),當d≠0時,an 是關于n 的一次式,它的圖象是一條直線上,那么n 為自然數的點的集合.
(3)對于A 是a、b 的等差中項,可以表示成2 A=a+b。
(4)等差數列的前n 項和公式Sn=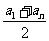 ·n-na1+
·n-na1+ d,可以整理成Sn=
d,可以整理成Sn=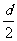 n2+
n2+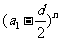 。當d≠0時是n 的一個常數項為0的二次式。
。當d≠0時是n 的一個常數項為0的二次式。
(5)等差數列的判定方法:
①定義法:對于數列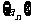 ,若
,若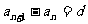 (常數),則數列
(常數),則數列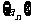 是等差數列;
是等差數列;
②等差中項:對于數列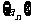 ,若
,若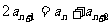 ,則數列
,則數列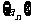 是等差數列。
是等差數列。
1.數列的知識要點:
(1)數列是特殊的函數,數列是定義在自然數集N(或它的有限子集{1,2,3,…,n,…})上的函數f(n),當自變量從小到大依次取值時對應的一列函數值:f(1),f(2),f(3),…,f(n),…。數列的圖象是由一群孤立的點構成的。
(2)對于數列的通項公式要掌握:①已知數列的通項公式,就可以求出數列的各項;②根據數列的前幾項,寫出數列的一個通項公式,這是一個難點,在學習中要注意觀察數列中各項與其序號的變化情況,分解所給數列的前幾項,看看這幾項的分解中.哪些部分是變化的,哪些是不變的,再探索各項中變化部分與序號的聯系,從而歸納出構成數列的規律,寫出通項公式;③一個數列還可以用遞推公式來表示;④在數列{an}中,前n 項和Sn 與通項公式an 的關系,是本講內容一個重點,要認真掌握之。即an=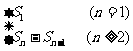 。特別要注意的是,若a1 適合由an=Sn-Sn-1(n≥2)可得到的表達式,則an 不必表達成分段形式,可化統一為一個式子.
。特別要注意的是,若a1 適合由an=Sn-Sn-1(n≥2)可得到的表達式,則an 不必表達成分段形式,可化統一為一個式子.
題型1:數列概念
(2009安徽卷文)已知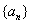 為等差數列,
為等差數列,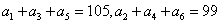 ,則
,則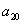 等于
等于
A. -1
B. 1 C. 3 D.7
[解析]∵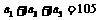 即
即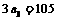 ∴
∴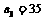 同理可得
同理可得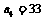 ∴公差
∴公差 ∴
∴ .選B。
.選B。
[答案]B
2.根據數列前4項,寫出它的通項公式:
(1)1,3,5,7……;
(2)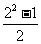 ,
,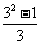 ,
,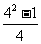 ,
,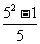 ;
;
(3) ,
,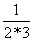 ,
,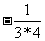 ,
,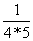 。
。
解析:(1)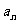 =2
=2 ; (2)
; (2)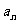 =
=  ; (3)
; (3)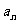 =
= 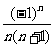 。
。
點評:每一項序號與這一項的對應關系可看成是一個序號到另一個數集的對應關系,這對考生的歸納推理能力有較高的要求。
例2.數列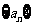 中,已知
中,已知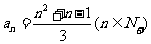 ,
,
(1)寫出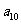 ,
,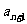 ,
,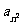 ; (2)
; (2)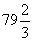 是否是數列中的項?若是,是第幾項?
是否是數列中的項?若是,是第幾項?
解析:(1)∵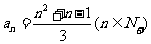 ,∴
,∴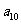
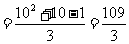 ,
,
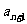
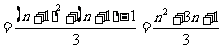 ,
,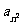
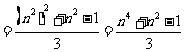 ;
; 
(2)令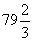
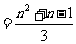 ,解方程得
,解方程得 ,
,
∵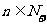 ,∴
,∴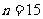 , 即
, 即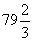 為該數列的第15項。
為該數列的第15項。
點評:該題考察數列通項的定義,會判斷數列項的歸屬.
 題型2:數列的遞推公式
題型2:數列的遞推公式
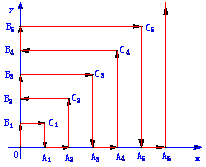
例3.如圖,一粒子在區域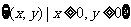 上運動,在第一秒內它從原點運動到點
上運動,在第一秒內它從原點運動到點 ,接著按圖中箭頭所示方向在x軸、y軸及其平行方向上運動,且每秒移動一個單位長度。
,接著按圖中箭頭所示方向在x軸、y軸及其平行方向上運動,且每秒移動一個單位長度。
(1)設粒子從原點到達點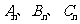 時,所經過的時間分別為
時,所經過的時間分別為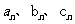 ,試寫出
,試寫出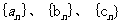 的通相公式;
的通相公式;
(2)求粒子從原點運動到點 時所需的時間;
時所需的時間;
(3)粒子從原點開始運動,求經過2004秒后,它所處的坐標。
解析:(1) 由圖形可設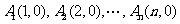 ,當粒子從原點到達
,當粒子從原點到達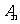 時,明顯有
時,明顯有




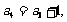

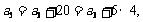
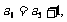

… …

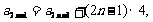


∴ =
= ,
,
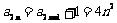 。
。
 ,
,
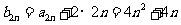 。
。
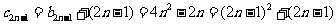 ,
,
 ,
,
即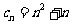 。
。

(2)有圖形知,粒子從原點運動到點 時所需的時間是到達點
時所需的時間是到達點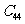 所經過得時間
所經過得時間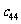 再加(44-16)=28秒,
再加(44-16)=28秒,
所以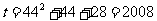 秒。
秒。
(3)由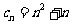
 2004,解得
2004,解得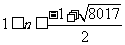 ,取最大得n=44,
,取最大得n=44,
經計算,得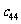 =1980<2004,從而粒子從原點開始運動,經過1980秒后到達點
=1980<2004,從而粒子從原點開始運動,經過1980秒后到達點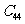 ,再向左運行24秒所到達的點的坐標為(20,44)。
,再向左運行24秒所到達的點的坐標為(20,44)。
點評:從起始項入手,逐步展開解題思維。由特殊到一般,探索出數列的遞推關系式,這是解答數列問題一般方法,也是歷年高考命題的熱點所在。
例4.(1)已知數列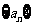 適合:
適合: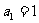 ,
,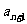
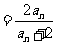 ,寫出前五項并寫出其通項公式;
,寫出前五項并寫出其通項公式;
(2)用上面的數列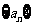 ,通過等式
,通過等式 構造新數列
構造新數列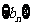 ,寫出
,寫出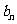 ,并寫出
,并寫出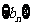 的前5項.
的前5項.
解:(1)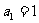 ,
,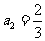 ,
,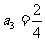 ,
,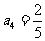 ,
, ,……,
,……,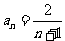 ;
;
(2)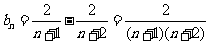 ,
,
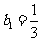 ,
,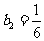 ,
,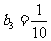 ,
,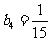 ,
,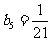 .
.
點評:會根據數列的前幾項寫出數列的一個通項公式,了解遞推公式是給出數列的又一種重要方法,能根據遞推公式寫出數列的前幾項。
題型3:數列的應用
例5.湖南省2008屆十二校聯考第一次考試
如果一個數列的各項都是實數,且從第二項開始,每一項與它前一項的平方差是相同的常數,則稱該數列為等方差數列,這個常數叫這個數列的公方差.
(1)設數列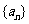 是公方差為
是公方差為 的等方差數列,求
的等方差數列,求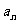 和
和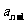
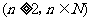 的關系式;
(2)若數列
的關系式;
(2)若數列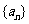 既是等方差數列,又是等差數列,證明該數列為常數列;
(3) 設數列
既是等方差數列,又是等差數列,證明該數列為常數列;
(3) 設數列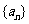 是首項為
是首項為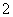 ,公方差為
,公方差為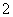 的等方差數列,若將
的等方差數列,若將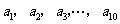 這種順
這種順
序的排列作為某種密碼,求這種密碼的個數.
(1)解:由等方差數列的定義可知: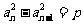
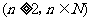 ………………5分
………………5分
(2)證法一:∵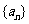 是等差數列,設公差為
是等差數列,設公差為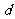 ,則
,則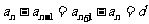 又
又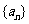 是等方差數列,∴
是等方差數列,∴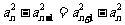 ………………………………7分
∴
………………………………7分
∴ 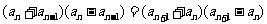 即
即 , …………………………………10分
∴
, …………………………………10分
∴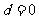 ,即
,即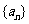 是常數列.…………………………………………………11分
證法二:∵
是常數列.…………………………………………………11分
證法二:∵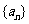 是等差數列,設公差為
是等差數列,設公差為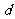 ,則
,則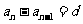 ……1
又
……1
又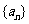 是等方差數列,設公方差為
是等方差數列,設公方差為 ,則
,則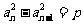 ……2…………7分
1代入2得,
……2…………7分
1代入2得,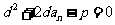 ……3
同理有,
……3
同理有, ……4
兩式相減得:即
……4
兩式相減得:即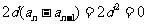 ,…………………………………10分
∴
,…………………………………10分
∴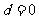 ,即
,即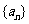 是常數列.………………………………………………11分
是常數列.………………………………………………11分
證法三:(接證法二1、2)
由1、2得出:若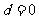 ,則
,則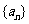 是常數列 …………………8分
是常數列 …………………8分
若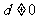 , 則
, 則 是常數, ∴
是常數, ∴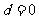 ,矛盾…………10分
,矛盾…………10分
∴ 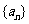 是常數列.
…………………11分
(3)依題意,
是常數列.
…………………11分
(3)依題意,

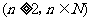 ,
,
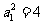 ,
,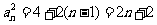 ∴
∴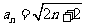 ,或
,或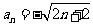 , ……………………………13分
即該密碼的第一個數確定的方法數是
, ……………………………13分
即該密碼的第一個數確定的方法數是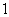 ,其余每個數都有“正”或“負”兩種
,其余每個數都有“正”或“負”兩種
確定方法,當每個數確定下來時,密碼就確定了,即確定密碼的方法數是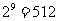 種,
故,這種密碼共
種,
故,這種密碼共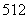 種.…………………………………………………16分
種.…………………………………………………16分
。
點評:解決此類問題的思路是先將實際問題轉化為數列模型來處理。
例6.在某報《自測健康狀況》的報道中,自測血壓結果與相應年齡的統計數據如下表.觀察表中數據的特點,用適當的數填入表中空白(_____)內.


答案:140 85
解析:從題目所給數據規律可以看到:收縮壓是等差數列.舒張壓的數據變化也很有規律:隨著年齡的變化,舒張壓分別增加了3毫米、2毫米,…照此規律,60歲時的收縮壓和舒張壓分別為140;85.
點評:本題以實際問題為背景,考查了如何把實際生活中的問題轉化為數學問題的能力.它不需要技能、技巧及繁雜的計算,需要有一定的數學意識,有效地把數學過程實施為數學思維活動。
題型4:等差數列的概念
例7.設Sn是數列{an}的前n項和,且Sn=n2,則{an}是( )
A.等比數列,但不是等差數列 B.等差數列,但不是等比數列
C.等差數列,而且也是等比數列 D.既非等比數列又非等差數列
答案:B;
解法一:an=
∴an=2n-1(n∈N)
又an+1-an=2為常數,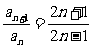 ≠常數
≠常數
∴{an}是等差數列,但不是等比數列.
解法二:如果一個數列的和是一個沒有常數項的關于n的二次函數,則這個數列一定是等差數列。
點評:本題主要考查等差數列、等比數列的概念和基本知識,以及靈活運用遞推式an=Sn-Sn-1的推理能力.但不要忽略a1,解法一緊扣定義,解法二較為靈活.
例8.設數列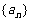 、
、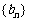 、
、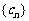 滿足:
滿足: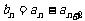 ,
, (n=1,2,3,…),證明:
(n=1,2,3,…),證明: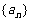 為等差數列的充分必要條件是
為等差數列的充分必要條件是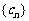 為等差數列且
為等差數列且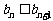 (n=1,2,3,…)
(n=1,2,3,…)
證明: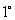 必要性:設數列
必要性:設數列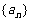 是公差為
是公差為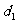 的等差數列,則:
的等差數列,則:
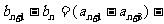
 =
=
 =
=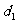 -
-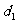 =0,
=0,
∴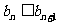 (n=1,2,3,…)成立;
(n=1,2,3,…)成立;
又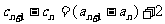

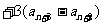 =6
=6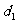 (常數)(n=1,2,3,…)
(常數)(n=1,2,3,…)
∴數列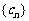 為等差數列。
為等差數列。
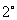 充分性:設數列
充分性:設數列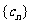 是公差為
是公差為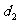 的等差數列,且
的等差數列,且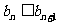 (n=1,2,3,…),
(n=1,2,3,…),
∵ ……① ∴
……① ∴ ……②
……②
①-②得:

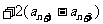
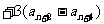 =
=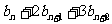
∵
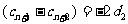
∴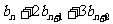
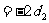 ……③ 從而有
……③ 從而有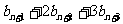
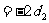 ……④
……④
④-③得: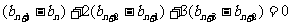 ……⑤
……⑤
∵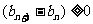 ,
, ,
, ,
,
∴由⑤得: (n=1,2,3,…),
(n=1,2,3,…),
由此,不妨設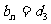 (n=1,2,3,…),則
(n=1,2,3,…),則
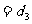 (常數)
(常數)
故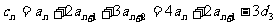 ……⑥
……⑥
從而
 ……⑦
……⑦
⑦-⑥得: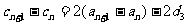 ,
,
故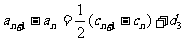
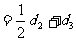 (常數)(n=1,2,3,…),
(常數)(n=1,2,3,…),
∴數列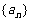 為等差數列。
為等差數列。
綜上所述: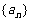 為等差數列的充分必要條件是
為等差數列的充分必要條件是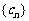 為等差數列且
為等差數列且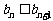 (n=1,2,3,…)。
(n=1,2,3,…)。
證法二:
令An = a n+1- a n,由b n≤b n+1知a n - a n+2≤a n+1- a n+3。
從而a n+1- a n≥a n+3 - a n+2,即An≥An+2(n=1,2,3,…)
由c n = a n + 2a n+1 + 3a n+2, c n+1 = 4a n+1 + 2a n+2 - 3 a n+3得
c n+1-c n=( a n+1- a n+2(a n+2- a n+1)+3(a n+3 - a n+2),即
An+2An+1+3An+2=d2. ⑥
由此得
An+2+2An+3+3An+2=d2. ⑦
⑥-⑦得
(An-An+2)+2(An+1- An+3)+3(An+2- An+4)=0 ⑧
因為An-An+2≥0,An+1- An+3≥0,An+2- An+4≥0,
所以由⑧得An-An+2=0(n=1,2,3,…)。
于是由⑥得
4An+2An+1=An+1+2An+2+3An+2=d2, ⑨
從而
2An+4An+1=4An+1+2An+2=d2 ⑩
由⑨和⑩得4An+2An+1=2An+4An+1,故An+1= An ,即
a n+2- a n+1= a n+1- a n(n=1,2,3,…),
所以數列{a n}是等差數列。
點評:該題考察判斷等差數列的方法,我們要講平時積累的方法巧妙應用,有些結論可以起到事半功倍的效果.
題型5:等差數列通項公式
例9.(2009天津卷文)已知等差數列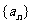 的公差d不為0,設
的公差d不為0,設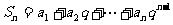
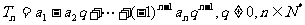
(Ⅰ)若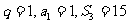 ,求數列
,求數列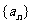 的通項公式;
的通項公式;
(Ⅱ)若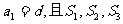 成等比數列,求q的值。
成等比數列,求q的值。
(Ⅲ)若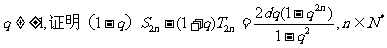
(1)解:由題設,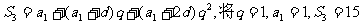
代入解得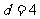 ,所以
,所以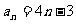
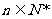
(2)解:當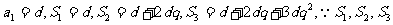 成等比數列,所以
成等比數列,所以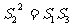 ,即
,即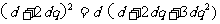 ,注意到
,注意到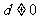 ,整理得
,整理得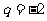
(3)證明:由題設,可得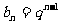 ,則
,則
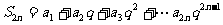 ①
①
 ②
②
①-②得,
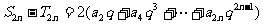
①+②得,
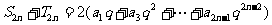 ③
③
③式兩邊同乘以 q,得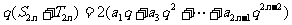
所以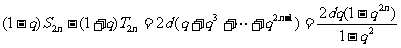
(3)證明: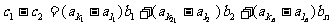
=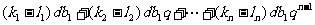
因為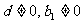 ,所以
,所以

若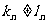 ,取i=n,
,取i=n,
若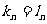 ,取i滿足
,取i滿足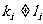 ,且
,且 ,
,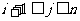
由(1)(2)及題設知,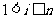 ,且
,且

①
當 時,
時,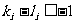 ,由
,由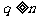 ,
,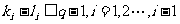
即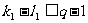 ,
,
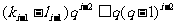
所以
因此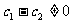
②
當 時,同理可得
時,同理可得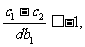 因此
因此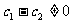
綜上,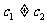
[考點定位]本小題主要考查了等差數列的通項公式,等比數列通項公式與前n項和等基本知識,考查運算能力和推理論證能力和綜合分析解決問題的能力.
例10.已知等比數列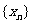 的各項為不等于1的正數,數列
的各項為不等于1的正數,數列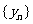 滿足
滿足 ,設
,設 。
。
(1)求數列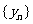 的前多少項和最大,最大值為多少?
的前多少項和最大,最大值為多少?
(2)試判斷是否存在自然數M,使當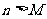 時,
時,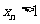 恒成立?若存在,求出相應的M,若不存在,請說明理由;
恒成立?若存在,求出相應的M,若不存在,請說明理由;
(3)令 ,試判斷數列
,試判斷數列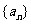 的增減性?
的增減性?
解:(1)由已知得: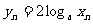
設等比數列{xn}的公比為q(q≠1)
由 得
得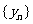 為等差數列,設公差為d
為等差數列,設公差為d
∵ ,∴d=-2; ∴
,∴d=-2; ∴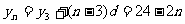
設前k項為最大,則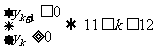
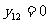
∴前11項和前12項和為最大,其和為132
(2)xn=a12-n,n∈N*; 若xn>1,則a12-n>1
當 時,n<12,顯然不成立 ; 當
時,n<12,顯然不成立 ; 當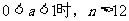
∴存在M=12,13,14,…,當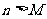 時,
時,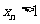
(3)an=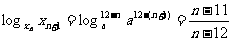
∵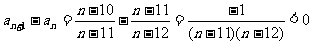
∴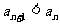 ∴
∴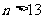 時數列{an}為遞減數列
時數列{an}為遞減數列
點評:該題通過求通項公式,最終通過通項公式解釋復雜的不等問題,屬于綜合性的題目,解題過程中注意觀察規律.
題型6:等差數列的前n項和公式
例11.(1)若一個等差數列前3項的和為34,最后3項的和為146,且所有項的和為390,則這個數列有( )
A.13項 B.12項 C.11項 D.10項
(2)設數列{an}是遞增等差數列,前三項的和為12,前三項的積為48,則它的首項是( )
A.1 B.2 C.4 D.6
(3))設Sn是等差數列{an}的前n項和,若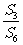 =
=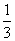 ,則
,則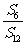 =( )
=( )
A.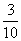 B.
B.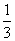 C.
C.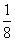 D.
D.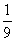
解析:(1)答案:A
設這個數列有n項
∵ ∴
∴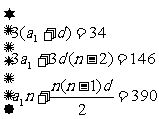
∴n=13
(2)答案:B
前三項和為12,∴a1+a2+a3=12,∴a2=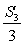 =4
=4
a1·a2·a3=48,∵a2=4,∴a1·a3=12,a1+a3=8,
把a1,a3作為方程的兩根且a1<a3,
∴x2-8x+12=0,x1=6,x2=2,∴a1=2,a3=6,∴選B.
(3)答案為A;
點評:本題考查了數列等差數列的前n項和公式的運用和考生分析問題、解決問題的能力.
例12.(1)設{an}為等差數列,Sn為數列{an}的前n項和,已知S7=7,S15=75,Tn為數列{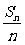 }的前n項和,求Tn。
}的前n項和,求Tn。
(2)已知數列{bn}是等差數列,b1=1,b1+b2+…+b10=100.
(Ⅰ)求數列{bn}的通項bn;
(Ⅱ)設數列{an}的通項an=lg(1+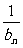 ),記Sn是數列{an}的前n項和,試比較Sn與
),記Sn是數列{an}的前n項和,試比較Sn與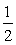 lgbn+1的大小,并證明你的結論。
lgbn+1的大小,并證明你的結論。
解析:(1)設等差數列{an}的公差為d,則
Sn=na1+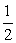 n(n-1)d.∴S7=7,S15=75,
n(n-1)d.∴S7=7,S15=75,
∴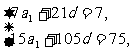 即
即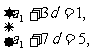
解得a1=-2,d=1.∴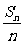 =a1+
=a1+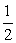 (n-1)d=-2+
(n-1)d=-2+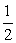 (n-1)。
(n-1)。
∵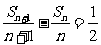 ,
,
∴數列{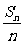 }是等差數列,其首項為-2,公差為
}是等差數列,其首項為-2,公差為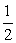 ,
,
∴Tn=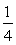 n2-
n2-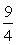 n.
n.
(2)(Ⅰ)設數列{bn}的公差為d,由題意得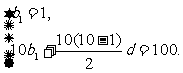
解得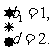 ∴bn=2n-1.
∴bn=2n-1.
(Ⅱ)由bn=2n-1,知
Sn=lg(1+1)+lg(1+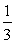 )+…+lg(1+
)+…+lg(1+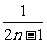 )
)
=lg[(1+1)(1+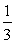 )…(1+
)…(1+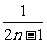 )],
)],
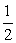 lgbn+1=lg
lgbn+1=lg .
.
因此要比較Sn與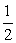 lgbn+1的大小,可先比較(1+1)(1+
lgbn+1的大小,可先比較(1+1)(1+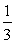 )…(1+
)…(1+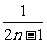 )與
)與 的大小.
的大小.
取n=1,有(1+1)>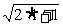 ,
,
取n=2,有(1+1)(1+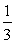 )>
)> ,……
,……
由此推測(1+1)(1+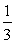 )…(1+
)…(1+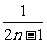 )>
)> . ①
. ①
若①式成立,則由對數函數性質可斷定:Sn>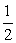 lgbn+1。
lgbn+1。
下面用數學歸納法證明①式。
(i)當n=1時已驗證①式成立。
(ii)假設當n=k(k≥1)時,①式成立,即(1+1)(1+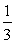 )…(1+
)…(1+ )>
)>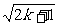 .
.
那么,當n=k+1時,(1+1)(1+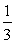 )…(1+
)…(1+ )[1+
)[1+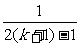 ]>
]>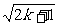
·(1+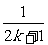 )=
)= (2k+2)。
(2k+2)。
∵[ (2k+2)]2-(
(2k+2)]2-(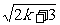 )2
)2
=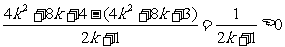 ,
,
∴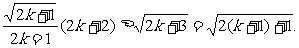 .
.
因而 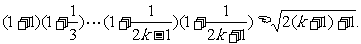
這就是說①式當n=k+1時也成立.
由(i),(ii)知①式對任何正整數n都成立.
由此證得:Sn>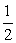 lgbn+1。
lgbn+1。
評述:本題主要考查等差數列的求和公式的求解和應用,對一些綜合性的問題要先理清思路再行求解.
題型7:等差數列的性質及變形公式
例13.(1)設{an}(n∈N*)是等差數列,Sn是其前n項的和,且S5<S6,S6=S7>S8,則下列結論錯誤的是( )
A.d<0 B.a7=0
C.S9>S5 D.S6與S7均為Sn的最大值
(2)等差數列{an}的前m項和為30,前2m項和為100,則它的前3m項和為( )
A.130 B.170 C.210 D.260
解析:(1)答案:C;
由S5<S6得a1+a2+a3+…+a5<a1+a2+…+a5+a6,∴a6>0,
又S6=S7,∴a1+a2+…+a6=a1+a2+…+a6+a7,∴a7=0,
由S7>S8,得a8<0,而C選項S9>S5,即a6+a7+a8+a9>0 2(a7+a8)>0,
2(a7+a8)>0,
由題設a7=0,a8<0,顯然C選項是錯誤的。
(2)答案:C
解法一:由題意得方程組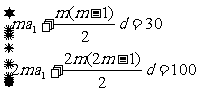 ,
,
視m為已知數,解得 ,
,
∴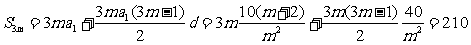 。
。
解法二:設前m項的和為b1,第m+1到2m項之和為b2,第2m+1到3m項之和為b3,則b1,b2,b3也成等差數列。
于是b1=30,b2=100-30=70,公差d=70-30=40。
∴b3=b2+d=70+40=110
∴前3m項之和S3m=b1+b2+b3=210.
解法三:取m=1,則a1=S1=30,a2=S2-S1=70,從而d=a2-a1=40。
于是a3=a2+d=70+40=110.∴S3=a1+a2+a3=210。
點評:本題考查等差數列的基本知識,及靈活運用等差數列解決問題的能力,解法二中是利用構造新數列研究問題,等比數列也有類似性質.解法三中,從題給選擇支獲得的信息可知,對任意變化的自然數m,題給數列前3m項的和是與m無關的不變量,在含有某種變化過程的數學問題,利用不變量的思想求解,立竿見影。
例14.在XOY平面上有一點列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…,對每個自然數n,點Pn位于函數y=2000(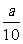 )x(0<a<10=的圖象上,且點Pn、點(n,0)與點(n+1,0)構成一個以Pn為頂點的等腰三角形。
)x(0<a<10=的圖象上,且點Pn、點(n,0)與點(n+1,0)構成一個以Pn為頂點的等腰三角形。
(Ⅰ)求點Pn的縱坐標bn的表達式;
(Ⅱ)若對每個自然數n,以bn,<
2.等差數列
(1)等差數列定義:一般地,如果一個數列從第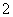 項起,每一項與它的前一項的差等于同一個常數,那么這個數列就叫等差數列,這個常數叫做等差數列的公差,公差通常用字母
項起,每一項與它的前一項的差等于同一個常數,那么這個數列就叫等差數列,這個常數叫做等差數列的公差,公差通常用字母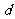 表示。用遞推公式表示為
表示。用遞推公式表示為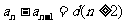 或
或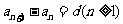 。
。
(2)等差數列的通項公式: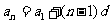 ;
;
說明:等差數列(通常可稱為
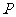 數列)的單調性:
數列)的單調性: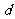
 為遞增數列,
為遞增數列,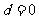 為常數列,
為常數列,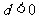 為遞減數列。
為遞減數列。
(3)等差中項的概念:
定義:如果 ,
, ,
,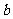 成等差數列,那么
成等差數列,那么 叫做
叫做 與
與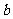 的等差中項。其中
的等差中項。其中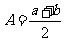
 ,
, ,
,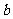 成等差數列
成等差數列
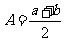 。
。
(4)等差數列的前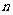 和的求和公式:
和的求和公式: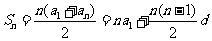 。
。
1.數列的概念
(1)數列定義:按一定次序排列的一列數叫做數列;
數列中的每個數都叫這個數列的項。記作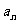 ,在數列第一個位置的項叫第1項(或首項),在第二個位置的叫第2項,……,序號為
,在數列第一個位置的項叫第1項(或首項),在第二個位置的叫第2項,……,序號為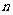 的項叫第
的項叫第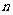 項(也叫通項)記作
項(也叫通項)記作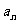 ;
;
數列的一般形式: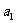 ,
,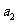 ,
, ,……,
,……,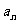 ,……,簡記作
,……,簡記作 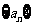 。
。
(2)通項公式的定義:如果數列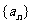 的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
例如,數列①的通項公式是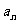 =
= 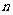 (
(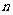
 7,
7,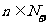 ),數列②的通項公式是
),數列②的通項公式是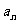 =
= 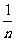 (
(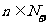 )。
)。
說明:①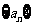 表示數列,
表示數列,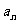 表示數列中的第
表示數列中的第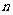 項,
項,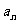 =
= 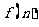 表示數列的通項公式;② 同一個數列的通項公式的形式不一定唯一。例如,
表示數列的通項公式;② 同一個數列的通項公式的形式不一定唯一。例如,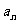 =
= 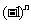 =
=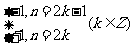 ; ③不是每個數列都有通項公式。例如,1,1.4,1.41,1.414,……
; ③不是每個數列都有通項公式。例如,1,1.4,1.41,1.414,……
(3)數列的函數特征與圖象表示:
序號:1
2 3 4 5 6
項 :4 5 6 7 8 9
上面每一項序號與這一項的對應關系可看成是一個序號集合到另一個數集的映射。從函數觀點看,數列實質上是定義域為正整數集 (或它的有限子集)的函數
(或它的有限子集)的函數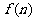 當自變量
當自變量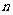 從1開始依次取值時對應的一系列函數值
從1開始依次取值時對應的一系列函數值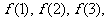 ……,
……,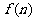 ,…….通常用
,…….通常用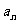 來代替
來代替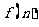 ,其圖象是一群孤立點。
,其圖象是一群孤立點。
(4)數列分類:①按數列項數是有限還是無限分:有窮數列和無窮數列;②按數列項與項之間的大小關系分:單調數列(遞增數列、遞減數列)、常數列和擺動數列.
(5)遞推公式定義:如果已知數列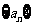 的第1項(或前幾項),且任一項
的第1項(或前幾項),且任一項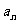 與它的前一項
與它的前一項 (或前幾項)間的關系可以用一個公式來表示,那么這個公式就叫做這個
數列的遞推公式.
(或前幾項)間的關系可以用一個公式來表示,那么這個公式就叫做這個
數列的遞推公式.
2.知識交匯的題目一般是數列與函數、不等式、解析幾何、應用問題聯系的綜合題,還可能涉及部分考察證明的推理題.
數列在歷年高考都占有很重要的地位,一般情況下都是一至二個客觀性題目和一個解答題。對于本將來講,客觀性題目主要考察數列、等差數列的概念、性質、通項公式、前n項和公式等基本知識和基本性質的靈活應用,對基本的計算技能要求比較高.
預測2010年高考:
1.題型既有靈活考察基礎知識的選擇、填空,又有關于數列推導能力或解決生產、生活中的實際問題的解答題;
3.能在具體的問題情境中,發現數列的等差關系,并能用有關知識解決相應的問題。體會等差數列與一次函數的關系.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com