日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

48.答案：B

解法一：由f(x)得：f^－1(x)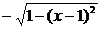＝(0≤x≤1)，故選B.

解法二：由f(x)得：x²+(y－1)²＝1，其中x∈［－1，0］，y∈［0，1］，其圖象為A.根據原函數與其反函數的圖象關于直線y=x對稱，可知f^－1(x)的圖象應為B.

評述：本題主要考查反函數的概念，要求對原函數與其反函數的聯系有深刻理解，并考查數形結合思想.

47.答案：B

解析：因為a＞1，所以y=log_ax為增函數，故C、D均不對，又1－a＜0，所以直線應過原點且經過第二象限和第四象限，故應選B.

46.答案：A

解析：用排除法.∵0<a<1，∴0<1－a<1，1+a>1，∴(1－a)>(1－a)成立，又

log_(1－a)(1+a)<0，排除B；(1－a)³<1而(1+a)²>1，∴(1－a)³<(1+a)²，排除C；又(1－a)^(1+a)<1，排除D.因此選A.

評述：本題考查指數函數和對數函數的基本性質.考查考生的邏輯思維能力.

45.答案：B

解法一：先求函數的定義域，由2－ax＞0，有ax＜2，因為a是對數的底，故有a＞0，于是得函數的定義域x≤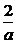，又函數的遞減區間［0，1］必須在函數的定義域內，故有1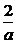＜，從而a＜2.

若1＜a＜2，當x在［0，1］上增大時，2－ax減小，從而log_a(2－ax)減小，即函數y=log_a(2－ax)在［0，1］上是單調遞減的；

若0＜a＜1，當x在［0，1］上增大時，2－ax減小，從而log_a(2－ax)增大，即函數y＝log_a(2－ax)在［0，1］上是單調遞增的.

所以a的取值范圍應是(1，2)，故選擇B.

解法二：因a是對數函數的底數，故a＞0，且a≠1，排除C；當0≤x≤1時，真數2－ax＞0，取x=1，得a＜2，排除D.取a＝時，函數y＝log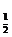(2－)，在區間［0，1］上，(2－)是x的減函數，故y是x的增函數，排除A，得B.

解法三：當a∈(0，1)時，若0≤x₁＜x₂≤1，則2－ax₁＞2－ax₂＞0，故log_a(2－ax₁)＜log_a(2－ax₂)，即y＝log_a(2－ax)在［0，1］上是x的增函數，排除A、C.當a＞2時，函數y在x=1處無定義，排除D，得B.

解法四：取a=，x₁＝0，x₂＝1，則有log_a(2－ax₁)＝log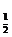2，log_a(2－ax₂)＝log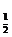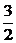，可排除A、C；取a=3，x=1，則2－ax＝2－3＜0，又y在x=1處有意義，故a≠3，排除D，得B.

解法五：因為a是對數的底．故有a＞0，∴u＝2－ax是減函數

又∵y＝log_a(2－ax)是減函數，由復合函數的增減性可知y＝log_au是增函數，

∴a＞1

又∵0≤x≤1，∴0≤ax≤a，0≥－ax≥－a，2≥2－ax≥2－a

又∵2－ax＞0，∴2－a＞0，∴a＜2，∴1＜a＜2．

解法六：因為a是對數的底數，故有a＞0，∴u=2－ax是減函數，又y=log_a(2－ax)是減函數，由復合函數的增減性，可知y=log_au是增函數，∴a＞1，又2－ax＞0，ax＜2，

x∈［0，1］

當x≠0時，a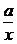＜，而對x∈(0，1］中每一值不等式都成立，a只需要小于其最小值即可，故a＜2，∴1＜a＜2，∴u=2－ax是減函數，∴y=log_a(2－ax)是減函數.

評述：本題主要考查對數函數的單調性和邏輯思維能力.入手思路寬.由常規的具體函數判定其單調性，換為由函數的單調性反過來確定函數中底數a的范圍，提高了思維層次，同時要求對對數函數的概念和性質有較深刻全面地理解并熟練掌握.

44.答案：B

解法一：取a=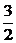代入可排除A、C，取a=3代入排除D，故答案為B.

方法二：因u＝2－x是x的減函數，要使y＝log_a(2－x)是x的增函數，只要0＜a＜1，答案為B.

評述：本題主要考查對數函數的單調性及分析問題、解決問題的能力.

43.答案：D

解析：把反比例函數y=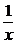的圖象向左平移1個單位就得到y=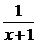的圖象.故選D.

評述：本題的選擇支不變，而題干改變為：“函數y=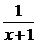－的圖象是……”，這正是1995年理科題，只須將y=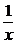－的圖象左移1個單位.2002年又討論過函數y=1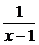－的圖象.說明(1)y=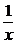的性質比較重要，圖形變換應熟練；(2)高考題中重點知識反復考，應對高考題吃深吃透.對參加高考是有極大幫助的.

42.答案：A

解析：A中直線a＞0，1＞b＞0，指數函數當a＞0，1＞b＞0時，0＜b^a＜1，故A正確；B、C、D中可分別考慮a，b的取值范圍，得出它們的圖象都是錯誤的.

41.答案：D

解析：由已知0＜1－a＜1，可推得A、C均錯，又1＜1+a＜1+b，有(1+a)^a＜

(1+b)^a＜(1+b)^b，故B錯，所以選D.

40.答案：A

解析一：由指數函數圖象可以看出0<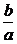<1.拋物線方程是y=a(x+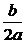)²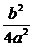－，其頂點坐標為(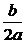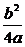－，－)，又由0<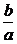<1，可得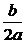－<－<0.觀察選擇支，可選A.

解析二：求y=ax²+bx與x軸的交點，令ax²+bx=0，解得x=0或x=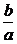－，而－1<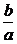－<0.故選A.

評述：本題雖小，但一定要細致觀察圖象，注意細微之處，獲得解題靈感.

39.答案：A

解析：當a＞1時，y＝log_ax單調遞增，y＝a^-x單調遞減，故選A.

評述：本題主要考查指數函數、對數函數的圖象及性質，源于課本，考查基本知識，難度不大.