
21.(本小題10分)
已知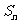 為等差數列
為等差數列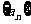 的前
的前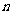 項和,
項和,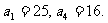
⑴求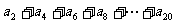 的值;
的值;
⑵求數列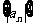 的前
的前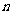 項和
項和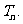
20.(本小題8分)
設等差數列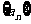 的前n項和為
的前n項和為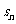 ,已知
,已知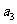 =12,且
=12,且 。
。
(1)求公差d的范圍;
(2)前幾項和最大?并說明理由。
19.(本小題8分)
△ABC中,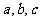 分別是A,B,C所對的邊,S是該三角形的面積,且
分別是A,B,C所對的邊,S是該三角形的面積,且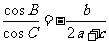
(1)求∠B的大小;
(2)若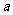 =4,
=4,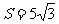 ,求
,求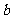 的值。
的值。
18.(本小題8分)
數列{ a n }的前項和為S n = 4n 2 – n + 2,求該數列的通項公式.
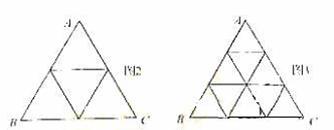
17.將正⊿ABC分割成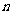
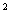 (
(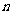 ≥2,n∈N)個全等的小正三角形(圖2,圖3分別給出了n=2,3的情形),在每個三角形的頂點各放置一個數,使位于⊿ABC的三遍及平行于某邊的任一直線上的數(當數的個數不少于3時)都分別依次成等差數列,若頂點A ,B ,C處的三個數互不相同且和為1,記所有頂點上的數之和為f(n),則有f(2)=2,則f(3)= .
≥2,n∈N)個全等的小正三角形(圖2,圖3分別給出了n=2,3的情形),在每個三角形的頂點各放置一個數,使位于⊿ABC的三遍及平行于某邊的任一直線上的數(當數的個數不少于3時)都分別依次成等差數列,若頂點A ,B ,C處的三個數互不相同且和為1,記所有頂點上的數之和為f(n),則有f(2)=2,則f(3)= .
16.數列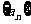 中,
中, ,
,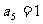 ,數列
,數列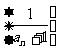 是等差數列,則
是等差數列,則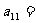
15. 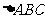 中,若b=2a , B=A+60°,則A=
.
中,若b=2a , B=A+60°,則A=
.
14.△ABC中,已知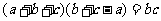 ,則A的度數等于
,則A的度數等于
13.《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數學著作之一。書中有一道這樣的題目:把100個面包分給五人,使每人成等差數列,且使最大的三份之和的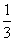 是較小的兩份之和,則最小1份的大小是
是較小的兩份之和,則最小1份的大小是
12. 在等差數列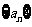 中,
中,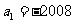 ,其前
,其前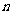 項的和為
項的和為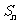 .若
.若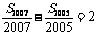 ,則
,則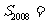 (
)
(
)
A.-2007 B.-2008 C.2007 D.2008
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com