
8.This is a very common word,________(尤其)in spoken English.
7.The country depends on ________(旅游業)for most of its income.
6.His score is now well into double ________(數字).
5.Many c________ sent money to help the refugees(難民).
4.Can I e________ pounds for dollars here?
3.Indians are the first i________ of North America.
2.A child receives its early e________ from its parents at home.
1.We m________ the room and found it was 20 feet long and 15 feet wide.
常用的抽樣方法及它們 之間的聯系和區別:
之間的聯系和區別:
|
類別 |
共同點 |
各自  特點 特點 |
相互聯系 |
適用范圍 |
|
簡單隨機抽樣 |
抽樣過程中每個個體被抽取的概率是相同的 |
從總體中逐個抽取 |
|
總體中的個數比較少 |
|
系統抽樣 |
將總體均勻分成幾個部分,按照事先確定的規則在各部分抽取 |
在起始部分抽樣時采用簡單隨機抽樣 |
總體中的個數比較多 |
|
|
分層抽樣 |
將總體分成幾層,分層進行抽取 |
各層抽樣時采用簡單抽樣或者相同抽樣 |
總體由差異明顯的幾部分組成 |
不放回抽樣和放回抽樣:在抽樣中,如果每次抽出個體后不再將它放回總體,稱這樣的抽樣為不放回抽樣;如果每次抽出個體后再將它放回總體,稱這樣的抽樣為放回抽樣。
隨機抽樣、系統抽樣、分層抽樣都是不放回抽樣
題型1:統計概念及簡單隨機抽樣
例1.為調查參加運動會的1000名運動員的年齡情況,從中抽查了100名運動員的年齡,就這個問題來說,下列說法正確的是( )
A.1000名運動員是總體 B.每個運動員是個體
C.抽取的100名運動員是樣本 D.樣本容量是100
解 析:這個問題我們研究的是運動員的年齡情況,因此應選D。
析:這個問題我們研究的是運動員的年齡情況,因此應選D。
答案:D
點評:該題屬于易錯題,一定要區分開總體與總體容量、樣本與樣本容量等概念。
例2.今 用簡單隨機抽樣從含有6個個體的總體中抽取一個容量為2的樣本。問:①
總體中的某一個體
用簡單隨機抽樣從含有6個個體的總體中抽取一個容量為2的樣本。問:①
總體中的某一個體 在第一次抽取時被抽到的概率是
在第一次抽取時被抽到的概率是 多少?② 個體
多少?② 個體 不是在第1次未被抽到,而是在第2次被抽到的概率是多少?③ 在整個抽樣過程中,個體
不是在第1次未被抽到,而是在第2次被抽到的概率是多少?③ 在整個抽樣過程中,個體 被抽到的概率是多少?
被抽到的概率是多少?
解析:(1) ,(2)
,(2) ,(3)
,(3) 。
。
點評:由問題(1)的解答,出示簡單隨機抽樣的定義,問題( 2 )是本講難點。基于此,簡單隨機抽樣體現了抽樣的客觀性與公平性
題型2:系統抽樣
例3.為了 了解參加某種知識競賽的1003名學生的成績,請用系統抽樣抽取一個容量為50的樣本。
了解參加某種知識競賽的1003名學生的成績,請用系統抽樣抽取一個容量為50的樣本。
解析:(1)隨機地將這1003個個體編號為1,2,3,…,1003.
(2)利用簡單隨機抽樣,先從總體中剔除3個個體(可利用隨機數表),剩下的個體數1000能被樣本容量50整除,然后再按系統抽樣的方法進行.
點評:總體中的每個個體被剔除的概率相等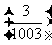 ,也就是每個個體不被剔除的概率相等
,也就是每個個體不被剔除的概率相等 .采用系統抽樣時每個個體被抽取的概率都是
.采用系統抽樣時每個個體被抽取的概率都是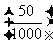 ,所以在整個抽樣過程中每個個體被抽取的概率仍然相等,都是
,所以在整個抽樣過程中每個個體被抽取的概率仍然相等,都是 。
。
例4.(2008年湖南理,15)
.對有n(n≥4)個元素的總體 進行抽樣,先將總體分成兩個子總體
進行抽樣,先將總體分成兩個子總體
 和
和 (m是給定的正整數,且2≤m≤n-2),再從
(m是給定的正整數,且2≤m≤n-2),再從
每個子總體中各隨機抽取2個元素組成樣本.用 表示元素i和j同時出現在樣
表示元素i和j同時出現在樣
本中的概率,則 =
; 所有
=
; 所有 (1≤i<j≤
(1≤i<j≤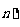 的和等于
.
的和等于
.
[答案]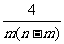 , 6
, 6
[解析]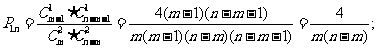 第二空可分:
第二空可分:
①當 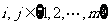 時,
時, 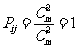 ;
;
②當 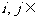
 時,
時,  ;
;
③當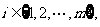
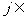
 時,
時, 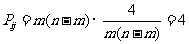 ;
;
所以
點評:當總體中個體個數較多而差異又不大時可采用系統抽樣。采用系統抽樣在每小組內抽取時應按規則進行
(2009年廣東卷文)(本小題滿分13分)
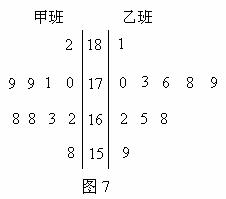 隨機抽取某中學甲乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖
隨機抽取某中學甲乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖
如圖7.
(1)根據莖葉圖判斷哪個班的平均身高較高;
(2)計算甲班的樣本方差
(3)現從乙班這10名同學中隨機抽取兩名身高不低于
173cm的同學,求身高為176cm的同學被抽中的概率.
解析 (1)由莖葉圖可知:甲班身高集中于
之間,而乙班身高集中于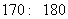 之間。因此乙班平
之間。因此乙班平
均身高高于甲班;
(2) 
甲班的樣本方差為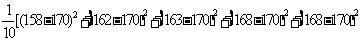
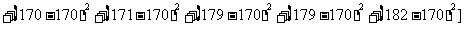 =57
=57
(3)設身高為176cm的同學被抽中的事件為A;
從乙班10名同學中抽中兩名身高不低于173cm的同學有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10個基本事件,而事件A含有4個基本事件;
 ;
;
題型3:分層抽樣
例5.(2009全國卷Ⅱ文)(本小題滿分12分)某車間甲組有10名工人,其中有4名女工人;
乙組有10名工人,其中 有6名女工人。現采用分層抽樣(層內采用不放回簡單隨即抽樣)從甲、乙兩組中共抽取4名工人進行技術考核
有6名女工人。現采用分層抽樣(層內采用不放回簡單隨即抽樣)從甲、乙兩組中共抽取4名工人進行技術考核
(1)求從甲、乙兩組各抽取的人數;
(2)求從甲組抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率
 解析 本題考查概率統計知識,要求有正確理解分層抽樣的方法及利用分類原理處理事件概率的能力,第一問直接利用分層統計原理即可得人數,第二問注意要用組合公式得出概率,第三問關鍵是理解清楚題意以及恰有2名男工人的具體含義,從而正確分類求概率.
解析 本題考查概率統計知識,要求有正確理解分層抽樣的方法及利用分類原理處理事件概率的能力,第一問直接利用分層統計原理即可得人數,第二問注意要用組合公式得出概率,第三問關鍵是理解清楚題意以及恰有2名男工人的具體含義,從而正確分類求概率.
解 (1)由于甲、乙兩組各有10名工人,根據分層抽樣原理,要從甲、乙兩組中共抽
取4名工人進行技術考核,則從每組各抽取2名工人.
(2)記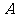 表示事件:從甲組抽取的工人中恰有1名女工人,則
表示事件:從甲組抽取的工人中恰有1名女工人,則
(3)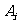 表示事件:從甲組抽取的2名工人中恰有
表示事件:從甲組抽取的2名工人中恰有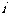 名男工人,
名男工人, [來源:]
[來源:]
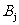 表示事件:從乙組抽取的2名工人中恰有
表示事件:從乙組抽取的2名工人中恰有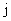 名男工人,
名男工人,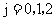
 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
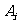 與
與 獨立,
獨立, ,且
,且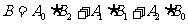
故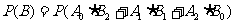

點評:本小題主要考查分層抽樣的概念和運算,以及運用統計知識解決實際問題的能力。
例6.甲校有3600名學生,乙校有5400名學生,丙校有1800名學生,為統計三校學生某方面的情況,計劃采用分層抽樣法,抽取一個樣本容量為90人的樣本,應在這三校分別抽取學生( )
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,10人 D.30人,50人,10人
解析:B;
點評:根據樣本容量和總體容量確定抽樣比,最終得到每層中學生人數。
題型4:綜合問題
例7.(1)某公司在甲、乙、丙、丁四個地區分別有150個、120個、180個、150個銷售點.公司為了調查產品銷售的情況,需從這600個銷售點中抽取一個容量為100的樣本,記這項調查為①;在丙地區中有20個特大型銷售點,要從中抽取7個調查其銷售收入和售后服務情況,記這項調查為②.則完成①、②這兩項調查宜采用的抽樣方法依次是
A.分層抽樣法,系統抽樣法 B.分層抽樣法,簡單隨機抽樣法
C.系統抽樣法,分層抽樣法 D.簡單隨機抽樣法, 分層抽樣法
分層抽樣法
分析:此題為抽樣方法的選取問題.當總體中個體較多時宜采用系統抽樣;當總體中的個體差異較大時 ,宜采用分層抽樣;當總體中個體較少時,宜采用隨機抽樣.
,宜采用分層抽樣;當總體中個體較少時,宜采用隨機抽樣.
依據題意,第①項調查應采用分層抽樣法、第②項調查應采用簡單隨機抽樣法.故選B.
答案:B
(2)某初級中學有學生270人,其中一年級108人,二、三年級各81人,現要利用抽樣方法抽取10人參加某項調查,考慮選用簡單隨機抽樣、分層抽樣和系統抽樣三種方案,使用簡單隨機抽樣和分層抽樣時,將學生按一、二、三年級依次統一編號為1,2,…,270;使用系統抽樣時,將學生統一隨機編號1,2,…,270,并將整個編號依次分為10段.如果抽得號碼有下列 四種情況:
四種情況:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
關于上述樣本的下列結論中,正確的是 ( )
A.②、③ 都不能為系統抽樣 B.②、④都不能為分層抽樣
都不能為系統抽樣 B.②、④都不能為分層抽樣
C.①、④都可能為系統抽樣 D.①、③都可能為分層抽樣
解析:D。
點評:采用什么樣的抽樣方法要依據研究的總體中的個體情況來定。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com