
4. Ladies and gentlemen,
please remain __________ until the plane has come to a complete stop.
A. seated B. seating C. to seat D. seat
3. I like this house with a
beautiful garden in front , but I don’t have enough money to buy__________.
A. one B. it C. this D. that
2. He told us whether
_________ a picnic was still under discussion
A. to have B. having C. have D. had
第一節
語法和詞匯知識(共20小題;每小題1分,滿分20分)
從A、B、C、D四個選項中,選出可以填入空白處的最佳選項,并在答題卡上將該項涂黑。
1. -May
I open the window to let in some fresh air ?
-___________
A. Come on B. Take care C. Go ahead! D. Hold on!
3.導數與解析幾何或函數圖象的混合問題是一種重要類型,也是高考中考察綜合能力的一個方向,應引起注意。
2.關于函數特征,最值問題較多,所以有必要專項討論,導數法求最值要比初等方法快捷簡便。
4.導數的常規問題:
(1)刻畫函數(比初等方法精確細微);
(2)同幾何中切線聯系(導數方法可用于研究平面曲線的切線);
(3)應用問題(初等方法往往技巧性要求較高,而導數方法顯得簡便)等關于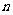 次多項式的導數問題屬于較難類型。
次多項式的導數問題屬于較難類型。
3.導數的應用:
①求切線的斜率。
②導數與函數的單調性的關系
㈠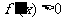 與
與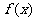 為增函數的關系。
為增函數的關系。
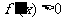 能推出
能推出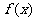 為增函數,但反之不一定。如函數
為增函數,但反之不一定。如函數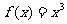 在
在 上單調遞增,但
上單調遞增,但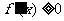 ,∴
,∴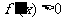 是
是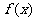 為增函數的充分不必要條件。
為增函數的充分不必要條件。
㈡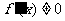 時,
時,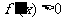 與
與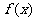 為增函數的關系。
為增函數的關系。
若將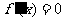 的根作為分界點,因為規定
的根作為分界點,因為規定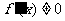 ,即摳去了分界點,此時
,即摳去了分界點,此時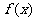 為增函數,就一定有
為增函數,就一定有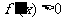 。∴當
。∴當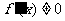 時,
時,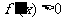 是
是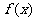 為增函數的充分必要條件。
為增函數的充分必要條件。
㈢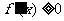 與
與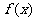 為增函數的關系。
為增函數的關系。
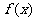 為增函數,一定可以推出
為增函數,一定可以推出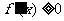 ,但反之不一定,因為
,但反之不一定,因為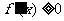 ,即為
,即為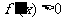 或
或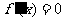 。當函數在某個區間內恒有
。當函數在某個區間內恒有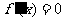 ,則
,則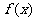 為常數,函數不具有單調性。∴
為常數,函數不具有單調性。∴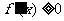 是
是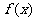 為增函數的必要不充分條件。
為增函數的必要不充分條件。
函數的單調性是函數一條重要性質,也是高中階段研究的重點,我們一定要把握好以上三個關系,用導數判斷好函數的單調性。因此新教材為解決單調區間的端點問題,都一律用開區間作為單調區間,避免討論以上問題,也簡化了問題。但在實際應用中還會遇到端點的討論問題,要謹慎處理。
㈣單調區間的求解過程,已知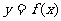 (1)分析
(1)分析
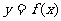 的定義域;(2)求導數
的定義域;(2)求導數  (3)解不等式
(3)解不等式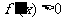 ,解集在定義域內的部分為增區間(4)解不等式
,解集在定義域內的部分為增區間(4)解不等式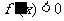 ,解集在定義域內的部分為減區間。
,解集在定義域內的部分為減區間。
我們在應用導數判斷函數的單調性時一定要搞清以下三個關系,才能準確無誤地判斷函數的單調性。以下以增函數為例作簡單的分析,前提條件都是函數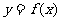 在某個區間內可導。
在某個區間內可導。
③求極值、求最值。
注意:極值≠最值。函數f(x)在區間[a,b]上的最大值為極大值和f(a) 、f(b)中最大的一個。最小值為極小值和f(a) 、f(b)中最小的一個。
f/(x0)=0不能得到當x=x0時,函數有極值。
但是,當x=x0時,函數有極值 f/(x0)=0
f/(x0)=0
判斷極值,還需結合函數的單調性說明。
2.導數的幾何物理意義:
k=f/(x0)表示過曲線y=f(x)上的點P(x0,f(x0))的切線的斜率。
V=s/(t) 表示即時速度。a=v/(t) 表示加速度。
1.求導法則:
(c)/=0 這里c是常數。即常數的導數值為0。
(xn)/=nxn-1 特別地:(x)/=1 (x-1)/= (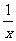 )/=-x-2 (f(x)±g(x))/=
f/(x)±g/(x) (k•f(x))/=
k•f/(x)
)/=-x-2 (f(x)±g(x))/=
f/(x)±g/(x) (k•f(x))/=
k•f/(x)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com