
5.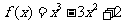 在區間
在區間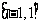 上的最大值是
上的最大值是
典型例題
一 導數的概念與運算
例1:如果質點A按規律s=2t3運動,則在t=3 s時的瞬時速度為
變式:定義在D上的函數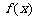 ,如果滿足:
,如果滿足: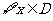 ,
,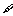 常數
常數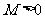 ,
,
都有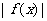 ≤M成立,則稱
≤M成立,則稱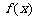 是D上的有界函數,其中M稱為函數的上界.
是D上的有界函數,其中M稱為函數的上界.
(1)若已知質點的運動方程為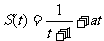 ,要使在
,要使在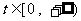 上的每一時刻的瞬時速度是以M=1為上界的有界函數,求實數a的取值范圍.
上的每一時刻的瞬時速度是以M=1為上界的有界函數,求實數a的取值范圍.
例:求所給函數的導數: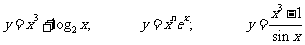 。
。
變式:設f(x)、g(x)分別是定義在R上的奇函數和偶函數,當x<0時,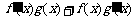 >0.且g(3)=0.則不等式f(x)g(x)<0的解集是
>0.且g(3)=0.則不等式f(x)g(x)<0的解集是
例2:已知函數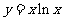 .(1)求這個函數的導數;(2)求這個函數在點
.(1)求這個函數的導數;(2)求這個函數在點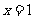 處的切線的方程.
處的切線的方程.
變式1:已知函數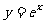 .
.
(1)求這個函數在點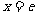 處的切線的方程;
處的切線的方程;
(2)過原點作曲線y=ex的切線,求切線的方程.
變式2:函數y=ax2+1的圖象與直線y=x相切,則a=
例3:判斷下列函數的單調性,并求出單調區間:

變式1:函數 的一個單調遞增區間是
的一個單調遞增區間是
變式2:已知函數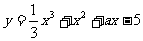
(1)若函數的單調遞減區間是(-3,1),則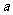 的是 .
的是 .
(2)若函數在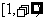 上是單調增函數,則
上是單調增函數,則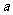 的取值范圍是
.
的取值范圍是
.
例4:求函數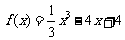 的極值.
的極值.
求函數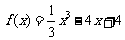 在
在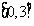 上的最大值與最小值..
上的最大值與最小值..
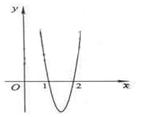 變式1:已知函數
變式1:已知函數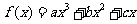 在點
在點 處取得極大值
處取得極大值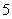 ,其導函數
,其導函數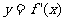 的圖象經過點
的圖象經過點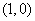 ,
,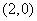 ,如圖所示.求:
,如圖所示.求:
(Ⅰ) 的值;(Ⅱ)
的值;(Ⅱ)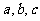 的值.
的值.
變式2:若函數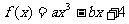 ,當
,當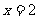 時,函數
時,函數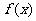 極值
極值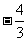 ,
,
(1)求函數的解析式;
(2)若函數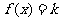 有3個解,求實數
有3個解,求實數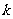 的取值范圍.
的取值范圍.
變式3:已知函數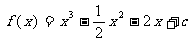 ,對xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范圍。
,對xÎ(-1,2),不等式f(x)<c2恒成立,求c的取值范圍。
實戰訓練
4.曲線 和
和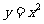 在它們交點處的兩條切線與
在它們交點處的兩條切線與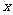 軸所圍成的三角形面積是
。
軸所圍成的三角形面積是
。
3.過點(-1,0)作拋物線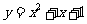 的切線,則其中一條切線為
的切線,則其中一條切線為
2.若曲線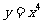 的一條切線
的一條切線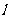 與直線
與直線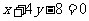 垂直,則
垂直,則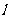 的方程為
的方程為
1.求下列函數導數
(1)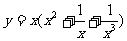 (2)
(2)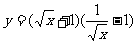
(3) (4)y=
(4)y=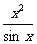
3.最值:
一般地,在區間[a,b]上連續的函數f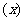 在[a,b]上必有最大值與最小值。
在[a,b]上必有最大值與最小值。
①求函數ƒ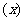 在(a,b)內的極值;
在(a,b)內的極值;
②求函數ƒ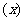 在區間端點的值ƒ(a)、ƒ(b);
在區間端點的值ƒ(a)、ƒ(b);
③將函數ƒ 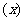 的各極值與ƒ(a)、ƒ(b)比較,其中最大的是最大值,其中最小的是最小值。
的各極值與ƒ(a)、ƒ(b)比較,其中最大的是最大值,其中最小的是最小值。
課前預習
2.極點與極值:
曲線在極值點處切線的斜率為0,極值點處的導數為0;曲線在極大值點左側切線的斜率為正,右側為負;曲線在極小值點左側切線的斜率為負,右側為正;
1.單調區間:一般地,設函數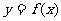 在某個區間可導,
在某個區間可導,
如果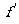
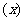
 ,則
,則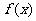 為增函數; 如果
為增函數; 如果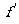
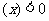 ,則
,則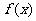 為減函數;
為減函數;
如果在某區間內恒有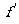
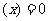 ,則
,則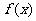 為常數;
為常數;
4.兩個函數的和、差、積的求導法則
法則1:兩個函數的和(或差)的導數,等于這兩個函數的導數的和(或差),
即:
(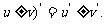
法則2:兩個函數的積的導數,等于第一個函數的導數乘以第二個函數,加上第一個
函數乘以第二個函數的導數,即: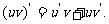
若C為常數,則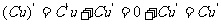 .即常數與函數的積的導數等于常數乘以函數的導數:
.即常數與函數的積的導數等于常數乘以函數的導數: 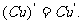
法則3:兩個函數的商的導數,等于分子的導數與分母的積,減去分母的導數與分子的積,再除以分母的平方: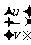 ‘=
‘=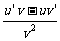 (v
(v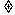 0)。
0)。
形如y=f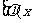
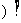 的函數稱為復合函數。復合函數求導步驟:分解--求導--回代。法則:y'|
的函數稱為復合函數。復合函數求導步驟:分解--求導--回代。法則:y'| = y'|
= y'|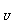 ·u'|
·u'|
導數應用
知識清單
3.幾種常見函數的導數:
① ②
② ③
③ ; ④
; ④ ;
;
⑤ ⑥
⑥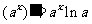 ; ⑦
; ⑦ ; ⑧
; ⑧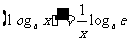 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com