日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

1.(★★★★★)Jumping out of airplane at ten thousand feet is quite________exciting experience.

　　 A.不填；the B.不填；an C.an；an D.the；the

(三)課堂小結：

　 1、求隨機事件概率的方法:

(1)通過大量重復試驗;

(2)等可能性事件的概率,也可以直接通過分析來計算其概率.

2、求等可能性事件概率的步驟：

(1)判斷所構造的基本事件是否等可能;

(2)計算一次試驗中可能出現的總結果數n;

(3)計算事件A所包含的結果數m;

(4)代入公式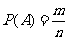計算;

(5)小結作答.

(二)例題示范，鞏固提高

例1、一個口袋內裝有大小相等的1個白球和已編有不同號碼的3個黑球，從中摸出2個球.

(1)共有多少種不同的結果？　　　　　　　　

(2)摸出2個黑球有多少種不同的結果？

(3)摸出2個黑球的概率是多少？　　

(學生舉手回答或個別提問，注意強調運用枚舉法和組合知識都可以來求結果數,另外在課件中體現集合思想的運用)

練習3、先后拋擲2枚均勻的硬幣

(1)一共可能出現　　　 種不同的結果;

(2)出現“1枚正面、1枚反面”的結果有　　　 種;

(3)出現“1枚正面、1枚反面”的概率是　　　 ;

(4)出現“兩枚都是反面”的概率是 　　　.

例2、將骰子先后拋擲2次，計算：

(1)一共有多少種不同的結果？

(2)其中向上的數之和是5的結果有多少種？

(3)向上的數之和是5的概率是多少？

　解：(1)將骰子拋擲1次，它落地時向上的數有1，2，3，4，5，6這6種結果.根據分步計數原理，先后將這個骰子拋擲2次，一共有6×6=36種不同的結果.

答：先后拋擲一個骰子2次， 一共有36種不同的結果.

(2)在上面所有結果中，向上的數之和是5的結果有(1，4)，(2，3)，(3，2)，(4，1)4種.

答：向上的數之和為5的結果有4種

(3)由于骰子是均勻的，將它拋擲2次的所有36種結果是等可能出現的.其中”向上的數之和是5”的結果(記為事件A)有4種，因此所求的概率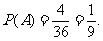

答：向上的數之和為5的概率是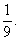

練習4、將一個正方體骰子先后拋擲2次，向上的數之和為5的倍數的概率是多少?

問題:現在你選擇作甲還是乙？為什么?

讓學生再選擇一次，并和開始的選擇對比.小組討論并說明理由.

通過對這個問題的解決,聯系我們的生活,同學們對學習數學有什么想法?

(小組討論--展示成果--教師總結)

教師總結時一定要把以下內容和學生的見解相結合.(學數學是有用的,處處留心皆數學.在生活中,如果適當地運用數學思維可以幫助我們更加理性地分析問題,對數學知識的合理運用能夠幫助我們作出更為合理的決策.

思維拓展：

(1)擲1個正四面體，落地時向下的數是3的概率是　　　　 ;

(2)將1個正四面體拋擲2次，落地時向下的數一個為1，另一個為3的概率是　　　 ;

(3)擲兩個正四面體，落地時向下的數一個為1，另一個為3的概率是　　　 ;

(4)擲兩個正四面體，落地時向下的數之和為4的概率是多少?

(一)設置情境，師生互動

(1)展示正方體的教具,讓學生猜:拋擲一次后,落地時向上的數是幾?先后拋擲兩次,落地時向上的數之和有幾種結果?

(2)課件展示游戲規則：將一個骰子先后拋擲兩次，若向上的數之和為5，6，7，8，則甲得1分；否則乙得1分.自今日起，每周做100次這個游戲，分數累積，一年之后分勝負(積分高者獲勝).

提出問題“你選擇作甲還是乙？”，并由此引出課題;

(3)通過對“拋擲一個骰子”的試驗結果的分析，由學生自主歸納基本事件、基本事件的概率;

(4)通過對練習1的求解,概括等可能性事件的概率的定義;

(5)通過對練習2的求解，讓學生知道如何從集合的角度理解等可能性事件的概率.

練習1、拋擲一個正方體骰子，

(1)落地時向上的數有　　 種結果;

(2)向上的數是3的倍數有　　 種結果；　

(3)向上的數是3的倍數的概率是　　　 .

練習2、一個口袋內裝有大小相等的1個白球和已編有不同號碼的3個黑球,從中摸出1個球,

(1)共有　　　 種不同的結果;

(2)摸出1個黑球有　　 種不同的結果;

(3)摸出1個黑球的概率是　　　 .

(1)配備多媒體設備的教學環境;

(2)PPT課件;

(3)自制一個正方體和一個正四面體的教具.

(1)以問題解決為主的教學策略：利用擲硬幣、摸球、擲骰子、擲正四面體這四種典型的等可能性事件概率模型，由淺到深，次數和個數由少到多的設置一系列問題，讓學生猜想、公式計算驗證猜想、反思歸納.

(2)自主合作學習策略：提出問題后，先給學生一定的獨立思考的時間，然后再安排小組討論,最后共同得出結論.

(1)高三的學生，已經學習過的內容再聽一遍，學生的心理狀況和情緒很難預測，臨場應變很關鍵.用到的排列、組合以及概率的知識應該都知道，理解不一定深刻;

(2)學生對隨機性的理解還不夠到位，用隨機觀念去描述和分析某些隨機現象的意識還不強，需在本節課繼續滲透.

(1)知識與技能目標：

了解等可能性事件的概率的意義，初步運用排列、組合的公式和枚舉法計算一些等可能性事件的概率.

(2)過程和方法目標：

通過學習、生活中的實際問題的引入，讓數學走進生活.將學生由對具體事例的感性認識上升到對定義的理性認識，可培養學生的梳理歸納能力；通過歸納定義后再加以應用可培養學生的信息遷移和類比推理能力；通過計算等可能性事件的概率，提高綜合運用排列、組合知識的能力和分析問題、解決問題的能力.

(3)情感與態度目標：

營造親切、和諧的氛圍，以“趣”激學；隨機事件的發生既有隨機性，又有規律性，使學生了解偶然性寓于必然性之中的辯證思想；引導學生樹立科學的人生觀和價值觀，培養學生的綜合素質.

(1)概述：《等可能性事件的概率》是全日制普通高級中學教科書(必修)第二冊(下B)第十一章概率第一節(第二課時)的內容.等可能性事件的概率是一種最基本的概率模型，它曾是概率論發展初期的主要研究對象，在概率論中占有相當重要的地位，它的引入，使我們可以解決一類隨機事件(等可能性事件)的概率，同時避免了大量的重復試驗.學好等可能性事件的概率可以為其它概率的學習奠定基礎，幫助學生進一步理解概率的意義，并能夠對生活中的一些現象作出解釋.

(2)教學重點：等可能性事件的概率的定義及其求法.

(3)教學難點：如何讓學生逐步掌握等可能性事件的概率計算的前提--每個結果出現的可能性必須相等.