
4. 從底角為
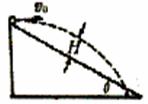
從底角為 的斜面頂端,以初速度v0水平拋出一小球,不計空氣阻力,若斜面足夠長,如圖所示,則小球拋出后,離開斜面的最大距離H為多少?
的斜面頂端,以初速度v0水平拋出一小球,不計空氣阻力,若斜面足夠長,如圖所示,則小球拋出后,離開斜面的最大距離H為多少?
3.如圖所示,傾角為 的斜面上方有一點O,在O點放一至斜面的光滑直軌道,要求一質點從O點沿直軌道到達斜面P點的時間最短.求該直軌道與豎直方向的夾角
的斜面上方有一點O,在O點放一至斜面的光滑直軌道,要求一質點從O點沿直軌道到達斜面P點的時間最短.求該直軌道與豎直方向的夾角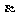 .
.
1.( )豎直向上的物體,初速與返回原地時的末速度大小之比為k,若在運動過程中空氣阻力大小不變,則空氣阻力與重力的大小之比為
A.k B.1/k C.(k2-1)/( k2+1) D.(k2+1)/( k2-1)
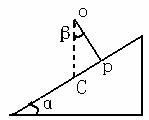
( ) 2.電容器C1、C2和可變電阻器R1、R2以及電源ε連接成如圖所示的電路.當R1的滑動觸頭在圖示位置時,C1、C2的電量相等.要使C1的電量大于C2的電量,應
2.電容器C1、C2和可變電阻器R1、R2以及電源ε連接成如圖所示的電路.當R1的滑動觸頭在圖示位置時,C1、C2的電量相等.要使C1的電量大于C2的電量,應
A.增大R2 B.減小R2
C.將R1的滑動觸頭向A端移動 D.將R1的滑動觸頭向B端滑動
4.函數求極值法
高考中對運用數學工具解決物理問題的要求越來越高,其中運用函數知識解決極值問題是常常遇到的.數學上求極值的方法通常有:利用二次函數求極值、利用不等式求極值、利用判別式求極值、利用三角函數求極值等.
 [例4]巡航快艇A從港口P出發攔截正以速度VB沿直線MN航行的船B,港口P與B船航線MN的垂直距離為a,A艇啟航時B船離港口的距離為b(b>a),如圖所示.如果略去A艇啟動時的加速過程,認為它始終做勻速運動,試求A艇能攔住B船所需的最小速率.
[例4]巡航快艇A從港口P出發攔截正以速度VB沿直線MN航行的船B,港口P與B船航線MN的垂直距離為a,A艇啟航時B船離港口的距離為b(b>a),如圖所示.如果略去A艇啟動時的加速過程,認為它始終做勻速運動,試求A艇能攔住B船所需的最小速率.
 [例5]如圖所示,一輛有四分之一圓弧的小車停在不光滑的水平地面上,質量為m的小球從靜止開始由車的頂端無摩擦滑下,且小車始終保持靜止狀態.試分析:當小球運動到什么位置時,地面對小車的靜摩擦力最大?最大值為多少?
[例5]如圖所示,一輛有四分之一圓弧的小車停在不光滑的水平地面上,質量為m的小球從靜止開始由車的頂端無摩擦滑下,且小車始終保持靜止狀態.試分析:當小球運動到什么位置時,地面對小車的靜摩擦力最大?最大值為多少?
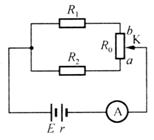
例6. 如圖所示,電源電動勢E=12 V,內阻r=0.5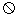 ,Rl=2
,Rl=2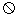 ,R2=3
,R2=3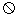 ,滑動變阻器的總電阻Ro=5
,滑動變阻器的總電阻Ro=5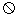 ,試分析:在滑動片K從a端移至b端的過程中,電流表A的示數如何變化?
,試分析:在滑動片K從a端移至b端的過程中,電流表A的示數如何變化?
強化訓練
3.特殊值法
有些問題直接計算可能非常繁瑣,但由于物理過程變化的有規律性,此時若取一個特殊值代入,得到的結論也應該是滿足的,這種方法尤其適用于選擇題的快速求解.
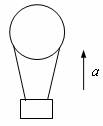
[例3]如圖所示,質量為M的氣球載有質量為m的沙袋,以加速度a上升,當將體積可忽略的沙袋拋出后,氣球上升的加速度將變為( )
 A.
A. B.
B.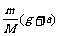
C.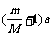 D.
D.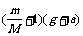
2.極端過程法
有些問題,對一般的過程分析求解難度很大,甚至中學階段暫時無法求出,可以把研究過程推向極端情況來加以考察分析,往往能很快得出結論.
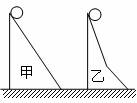
[例2]兩個光滑斜面,高度和斜面的總長度都相等,如圖所示,兩個相同的小球,同時由兩個斜面頂端由靜止開始釋放,不計拐角處能量損失,則兩球誰先到達底端?
1.極端值法
對于所考慮的物理問題,從它所能取的最大值或最小值方面進行分析,將最大值或最小值代入相應的表達式,從而得到所需的結論.
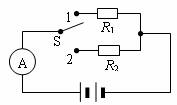
[例1]如圖所示,電源內阻不能忽略,R1=10Ω,R2=8Ω,當開關扳到位置1時,電流表的示數為0.2A;當開關扳到位置2時,電流表的示數可能是( )
 A.0.27A B.0.24A
A.0.27A B.0.24A
C.0.21A D.0.18A
通常情況下,由于物理問題涉及的因素眾多、過程復雜,很難直接把握其變化規律進而對其做出準確的判斷.但我們若將問題推到極端狀態、極端條件或特殊狀態下進行分析,卻可以很快得出結論.像這樣將問題從一般狀態推到特殊狀態進行分析處理的解題方法就是極端法.極端法在進行某些物理過程的分析時,具有獨特作用,恰當應用極端法能提高解題效率,使問題化難為易,化繁為簡,思路靈活,判斷準確.
用極端法分析問題,關鍵在于是將問題推向什么極端,采用什么方法處理.具體來說,首先要求待分析的問題有“極端”的存在,然后從極端狀態出發,回過頭來再去分析待分析問題的變化規律.其實質是將物理過程的變化推到極端,使其變化關系變得明顯,以實現對問題的快速判斷.通常可采用極端值、極端過程、特殊值、函數求極值等方法.
12.一物體作豎直上拋運動,經過高度為1.8m的窗戶歷時0.2s,則此物體上升到最高點與窗戶上端的距離是多少?(取g=10m/s2)
例題解析:
[例1][解析]由于小球脫離汽球后,先做豎直上拋運動再做自由落體運動,就全過程說是做勻變速直線運動,所以設小球在空中運動的總時間為t,若規定豎直向上的方向為正,則小球的位移s=-120m,v0=10m/s,a=-10m/s2,由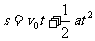 代入數據,解得t=6s。
代入數據,解得t=6s。
[例2][解析]人跌落后在重力作用下做自由落體運動,繩拉直后又受安全帶的作用,在重力和彈力共同作用下做變速直線運動,某瞬時速度變為零。
由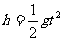 得自由落體時間:
得自由落體時間:
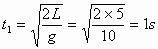
設安全帶對工人的平均沖力為F,對人下落的全過程應用動量定理得:
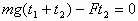
代入數據,解得F=1100N
[例3][解析]解法1:分段列式法.
選物體為研究對象,先研究自由落體過程,只有重力做功,設物體的質量為m,落到沙坑表面時速度為v,根據動能定理有:
mgH=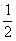 mv2-0 ①
mv2-0 ①
再研究物體在沙坑中的運動過程,重力做正功,阻力Ff做負功,根據動能定理有
mgh-Ff h=0-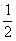 mv2 ②
mv2 ②
由①②兩式解得
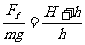
解法2:全程列式法
研究物體運動的全過程,據動能定理有:
mg(H+h)-Ff h=0
解得: =
=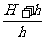
點評:若物體的運動過程包含幾個不同的物理過程,用動能定理解題時可以分段列方程,然后聯立求解.也可以視全過程為一整體列方程求解.當既能用“分段法”求解,又能用“全程法”求解時,一般來說,全程法比分段法簡捷.
[例4][解析]⑴對小球和桿A1組成的系統,由動量守恒定律得:
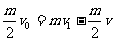 ①
①
又 s=vt ②
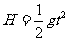 ③
③
①②③三式聯立解得: 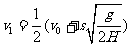 ④
④
回路內感應電動勢的最大值 E=BLv1 ⑤
回路內感應電流的最大值 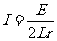 ⑥
⑥
④⑤⑥三式聯立解得: 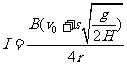
⑵兩棒組成的系統,對它們從開始作用到達到共同速度的全過程由動量守恒定律得:
mv1=2mv2
由能量守恒定律,整個運動過程中感應電流最多產生熱量為:
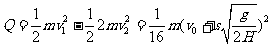
[例5][解析]若依據勻變速運動規律列式,將會出現總時間t比前后兩個5秒的和10秒是大還是小的問題:若t>10s將時間分為前5秒和后5秒與中間的時間t2,經復雜運算得t2=-2秒再得出t=8秒的結論。若用逆向的初速度為零的勻加速運動處理,將會簡便的多。
視為反向的初速度為零的加速直線運動
則最后5秒通過的路程: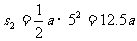
最初5秒通過的路程: 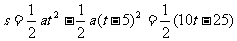
有題中已知的條件:s1:s2=11:5 得
(10t-25):25=11:25
11. 一個質量為
一個質量為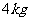 的物體靜止在足夠大的水平地面上,物體與地面間的動摩擦因數
的物體靜止在足夠大的水平地面上,物體與地面間的動摩擦因數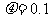 。從
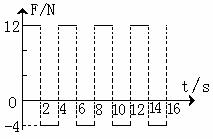
。從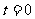 開始,物體受到一個大小和方向呈周期性變化的水平力F作用,力F隨時間的變化規律如圖所示。求83秒內物體的位移大小和力F對物體所做的功。
開始,物體受到一個大小和方向呈周期性變化的水平力F作用,力F隨時間的變化規律如圖所示。求83秒內物體的位移大小和力F對物體所做的功。 取10m/s2。
取10m/s2。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com