日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

5．一種元素的最高價氧化物和氣態化物的分子都是由極性鍵形成的非極性分子，這種元素是下列元素中的　　　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．硫　　　　　　　　　　　 B．磷　　　　　　　　　　　 C．碳　　　　　　　　　　　 D．氯

4．基態原子的4s能級中只有1個電子的元素共有　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．1種　　　　　　　　　 B．2種　　　　　　　　　　 C．3種　　　　　　　　　 D．8種

3．下列物質固態時一定是分子晶體的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．酸性氧化物　　　　　　　　　　　　　　　　　　　 B．堿性氧化物

　　　 C．含氧酸　　　　　　　　　　　　　　　　　　　　　　　 D．非金屬單質

2．下列化合物中含有手性碳原子的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．CCl₂F₂ B．

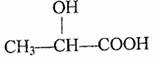
　　　 C．CH₃CH₂OH　　　　　　　　　　　　　　　　　　　 D．

1．下列敘述錯誤的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．¹³C和¹⁴C屬于同一種元素，它們互為同位素

　　　 B．¹H和²H是不同的核素，它們的質子數相等

　　　 C．¹⁴C和¹⁴N的質量數相等，它們的中子數不等

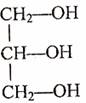　 　　　 D．⁶Li和⁷Li的電子數相等，中子數也相等

24．(本題滿分10分)

解：(1)證明：在Rt△FCD中，

∵G為DF的中點，

∴ CG= FD．………………1分

同理，在Rt△DEF中，　　

EG= FD．　 ………………2分

∴ CG=EG．…………………3分

(2)(1)中結論仍然成立，即EG=CG．…………………………4分

證法一：連接AG，過G點作MN⊥AD于M，與EF的延長線交于N點．

在△DAG與△DCG中，

∵ AD=CD，∠ADG=∠CDG，DG=DG，

∴ △DAG≌△DCG．

∴ AG=CG．………………………5分

在△DMG與△FNG中，

∵ ∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，

∴ △DMG≌△FNG．

∴ MG=NG

　 在矩形AENM中，AM=EN． ……………6分

在Rt△AMG 與Rt△ENG中，

∵ AM=EN， MG=NG，

∴ △AMG≌△ENG．

∴ AG=EG．

∴ EG=CG．　 ……………………………8分

證法二：延長CG至M,使MG=CG，

連接MF，ME，EC， ……………………4分

在△DCG 與△FMG中，

∵FG=DG，∠MGF=∠CGD，MG=CG，

∴△DCG ≌△FMG．

∴MF=CD，∠FMG＝∠DCG．　

∴MF∥CD∥AB．………………………5分

∴ ．

在Rt△MFE 與Rt△CBE中，

∵ MF=CB，EF=BE，

∴△MFE ≌△CBE．

∴ ．…………………………………………………6分

∴∠MEC＝∠MEF+∠FEC＝∠CEB+∠CEF＝90°．　 …………7分

∴ △MEC為直角三角形．

∵ MG = CG，

∴ EG= MC．

∴　 ．………………………………8分

(3)(1)中的結論仍然成立，

即EG=CG．其他的結論還有:EG⊥CG．……10分

23．(本題滿分10分)

解：(1)由題意，當MN和AB之間的距離為0.5米時，MN應位于DC下方，且此時△EMN中MN邊上的高為0.5米.

所以，S△EMN= =0.5(平方米).

即△EMN的面積為0.5平方米. …………2分

(2)①如圖1所示，當MN在矩形區域滑動，

即0＜x≤1時，　

△EMN的面積S= = ；……3分

②如圖2所示，當MN在三角形區域滑動，

即1＜x＜ 時，

如圖，連接EG，交CD于點F，交MN于點H，

∵ E為AB中點，

∴ F為CD中點，GF⊥CD,且FG＝ .

又∵ MN∥CD，

∴ △MNG∽△DCG．

∴　 ，即 ．……4分

故△EMN的面積S＝

＝ ； …………………5分

綜合可得：　

　　 ……………………………6分

(3)①當MN在矩形區域滑動時， ，所以有 ；………7分

②當MN在三角形區域滑動時，S= .

因而，當 (米)時,S得到最大值，

最大值S= = = (平方米).　 ……………9分

∵　 ，

∴ S有最大值，最大值為 平方米.　 ……………………………10分

22．(本題滿分10分)

解：延長BC交AD于E點，則CE⊥AD．……1分

在Rt△AEC中，AC＝10，

由坡比為1: 可知：∠CAE＝30°，………2分

∴ CE＝AC·sin30°＝10× ＝5，………3分

AE＝AC·cos30°＝10× ＝ ．……5分

在Rt△ABE中，

BE＝ ＝ =11．……………………………8分

∵ BE＝BC+CE，

∴ BC＝BE－CE＝11-5＝6(米)．　

答：旗桿的高度為6米． …………………………………………10分

21．(本題滿分9分)

解：(1)2007年銷量為a萬臺，則a(1+40%)=350，a =250(萬臺)．

…………………………………………………………………………3分

(2)設銷售彩電x萬臺，則銷售冰箱 x萬臺，銷售手機(350- x)萬臺．由題意得：1500x+2000× +800(350 x)=500000． ……………6分

解得x＝88．　 ………………………………………………………7分

∴　 ， ．

所以，彩電、冰箱(含冰柜)、手機三大類產品分別銷售88萬臺、132萬臺、130萬部．………………………………………………………………8分

∴ 88×1500×13%=17160(萬元)，132×2000×13%=34320(萬元)，

130×800×13%=13520(萬元)．　

獲得的政府補貼分別是17160萬元、34320萬元、13520萬元． ……9分

20．(本題滿分9分)

(1)解：在△AOC中，AC=2，

　　 ∵ AO＝OC＝2，

∴ △AOC是等邊三角形．………2分

∴ ∠AOC＝60°，

∴∠AEC＝30°．…………………4分

(2)證明：∵OC⊥l，BD⊥l．

∴ OC∥BD． ……………………5分

∴ ∠ABD＝∠AOC＝60°．

∵ AB為⊙O的直徑，

∴ △AEB為直角三角形，∠EAB＝30°．　 …………………………7分

　　 ∴∠EAB＝∠AEC．

　　 ∴ 四邊形OBEC 為平行四邊形．　 …………………………………8分

　　 又∵ OB＝OC＝2．　

　　 ∴ 四邊形OBEC是菱形．　 …………………………………………9分