
17.(2009四川卷文)(本小題滿分12分)
在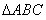 中,
中,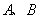 為銳角,角
為銳角,角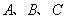 所對的邊分別為
所對的邊分別為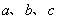 ,且
,且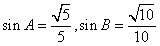
(I)求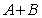 的值;
的值;
(II)若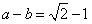 ,求
,求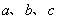 的值。
的值。
[解析](I)∵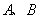 為銳角,
為銳角,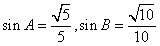
∴ 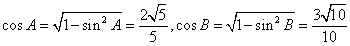
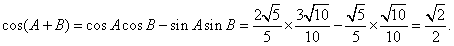
∵ 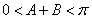
∴ 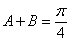 …………………………………………6分
…………………………………………6分
(II)由(I)知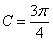 ,∴
,∴ 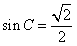
由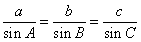 得
得
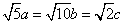 ,即
,即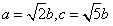
又∵
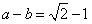
∴
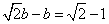 ∴
∴
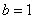
∴
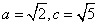 …………………………………………12分
…………………………………………12分
16.(2009天津卷文)(本小題滿分12分)
在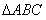 中,
中,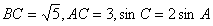
(Ⅰ)求AB的值。
(Ⅱ)求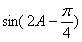 的值。
的值。
[答案]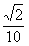
[解析](1)解:在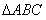 中,根據(jù)正弦定理,
中,根據(jù)正弦定理,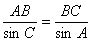 ,于是
,于是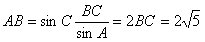
(2)解:在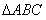 中,根據(jù)余弦定理,得
中,根據(jù)余弦定理,得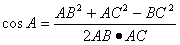
于是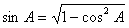 =
=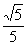 ,
,
從而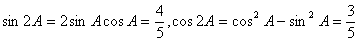
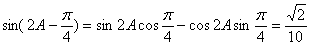
[考點定位]本題主要考查正弦定理,余弦定理同角的三角函數(shù)的關系式,二倍角的正弦和余弦,兩角差的正弦等基礎知識,考查基本運算能力。
15.(2009江西卷理)(本小題滿分12分)
△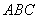 中,
中,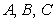 所對的邊分別為
所對的邊分別為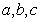 ,
,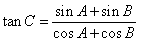 ,
,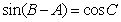 .
.
(1)求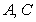 ;
;
(2)若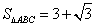 ,求
,求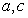 .
. 

解:(1) 因為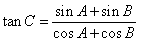 ,即
,即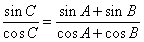 ,
,
所以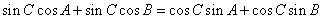 ,
,
即 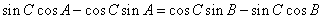 ,
,
得 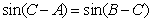 . 所以
. 所以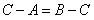 ,或
,或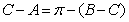 (不成立).
(不成立).
即 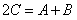 , 得
, 得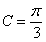 ,所以.
,所以.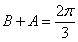
又因為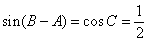 ,則
,則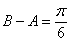 ,或
,或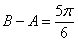 (舍去)
(舍去)
得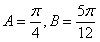
(2)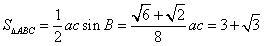 ,
,
又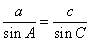 , 即
, 即 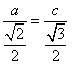 ,
, 

得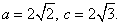
14.(2009江西卷文)(本小題滿分12分)
在△ 中,
中, 所對的邊分別為
所對的邊分別為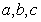 ,
,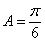 ,
,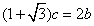 .
.
(1)求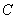 ;
;
(2)若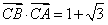 ,求
,求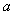 ,
,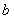 ,
,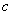 .
.
解:(1)由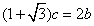 得
得 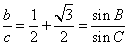
則有 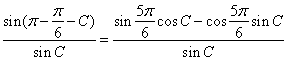 =
=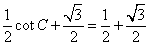
得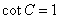 即
即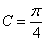 .
.
(2) 由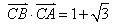 推出
推出 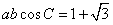 ;而
;而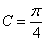 ,
,
即得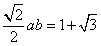 ,
,
則有 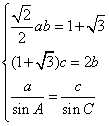 解得
解得 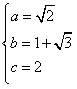
13.(2009安徽卷文)(本小題滿分12分)
在 ABC中,C-A=
ABC中,C-A=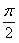 , sinB=
, sinB=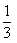 。
。
(I)求sinA的值;
(II)設AC=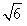 ,求
,求 ABC的面積。
ABC的面積。
[思路](1)依據(jù)三角函數(shù)恒等變形可得關于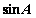 的式子,這之中要運用到倍角公式;
的式子,這之中要運用到倍角公式;
(2)應用正弦定理可得出邊長,進而用面積公式可求出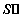 .
.
[解析](1)∵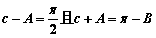 ∴
∴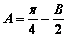
∴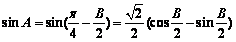


∴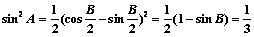
又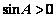 ∴
∴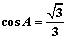
(2)如圖,由正弦定理得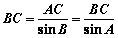 ∴
∴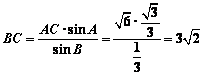
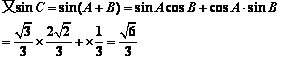
∴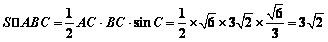 .
. 

12.(2009安徽卷理)(本小題滿分12分)
在 ABC中,
ABC中,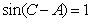 , sinB=
, sinB=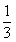 .
.
(I)求sinA的值;
(II)設AC=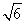 ,求
,求 ABC的面積.
ABC的面積.
本小題主要考查三角恒等變換、正弦定理、解三角形等有關知識,考查運算求解能力。本小題滿分12分
解:(Ⅰ)由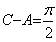 ,且
,且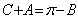 ,∴
,∴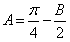 ,∴
,∴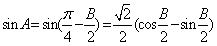 ,
,
 ∴
∴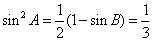 ,又
,又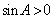 ,∴
,∴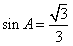
(Ⅱ)如圖,由正弦定理得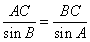
∴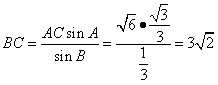 ,又
,又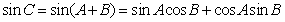
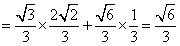
∴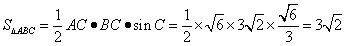


11.(2009廣東卷理)(本小題滿分12分)
已知向量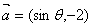 與
與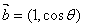 互相垂直,其中
互相垂直,其中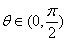 .
.
(1)求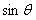 和
和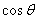 的值;
的值;
(2)若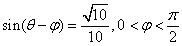 ,求
,求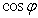 的值.
的值.
解:(1)∵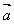 與
與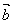 互相垂直,則
互相垂直,則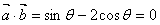 ,即
,即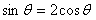 ,代入
,代入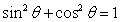 得
得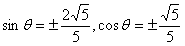 ,又
,又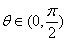 ,∴
,∴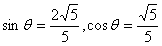 .
.
(2)∵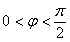 ,
,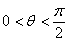 ,∴
,∴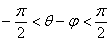 ,則
,則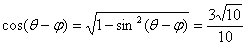 ,∴
,∴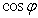
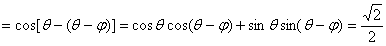 .
.
10.(2009全國卷Ⅱ文)(本小題滿分12分)設△ABC的內角A、B、C的對邊長分別為a、b、c,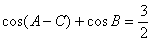 ,
,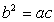 ,求B.
,求B.
解析:本題考查三角函數(shù)化簡及解三角形的能力,關鍵是注意角的范圍對角的三角函數(shù)值的制約,并利用正弦定理得到sinB=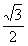 (負值舍掉),從而求出B=
(負值舍掉),從而求出B=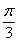 。
。
解:由 cos(A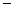 C)+cosB=
C)+cosB=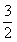 及B=π
及B=π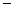 (A+C)得
(A+C)得
cos(A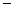 C)
C)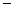 cos(A+C)=
cos(A+C)=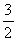 ,
,
cosAcosC+sinAsinC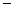 (cosAcosC
(cosAcosC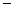 sinAsinC)=
sinAsinC)=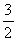 ,
,
sinAsinC=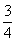 .
.
又由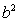 =ac及正弦定理得
=ac及正弦定理得 

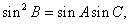
故 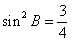 ,
,
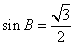 或
或 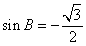 (舍去),
(舍去),
于是 B=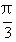 或 B=
或 B=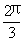 .
.
又由 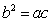 知
知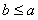 或
或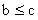
所以 B=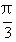 。
。
9.(2009山東卷文)(本小題滿分12分)設函數(shù)f(x)=2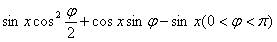 在
在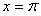 處取最小值.
處取最小值.
(3) 求 .的值;
.的值;
(4) 在 ABC中,
ABC中,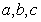 分別是角A,B,C的對邊,已知
分別是角A,B,C的對邊,已知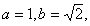
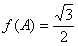 ,求角C..
,求角C..
解: (1)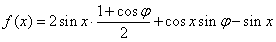
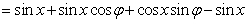
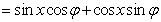
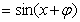
因為函數(shù)f(x)在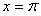 處取最小值,所以
處取最小值,所以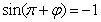 ,由誘導公式知
,由誘導公式知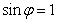 ,因為
,因為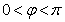 ,所以
,所以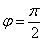 .所以
.所以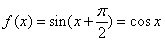


(2)因為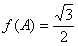 ,所以
,所以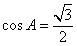 ,因為角A為
,因為角A為 ABC的內角,所以
ABC的內角,所以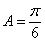 .又因為
.又因為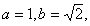 所以由正弦定理,得
所以由正弦定理,得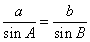 ,也就是
,也就是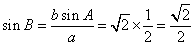 ,
,
因為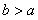 ,所以
,所以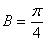 或
或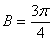 .
.
當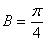 時,
時,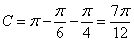 ;當
;當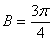 時,
時,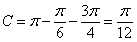 .
.
[命題立意]:本題主要考查了三角函數(shù)中兩角和差的弦函數(shù)公式、二倍角公式和三角函數(shù)的性質,并利用正弦定理解得三角形中的邊角.注意本題中的兩種情況都符合.
8.(2009山東卷理)(本小題滿分12分)設函數(shù)f(x)=cos(2x+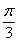 )+sin
)+sin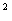 x.
x.
(1) 求函數(shù)f(x)的最大值和最小正周期.
(2) 設A,B,C為 ABC的三個內角,若cosB=
ABC的三個內角,若cosB=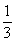 ,
,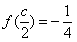 ,且C為銳角,求sinA.
,且C為銳角,求sinA.
解: (1)f(x)=cos(2x+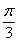 )+sin
)+sin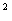 x.=
x.=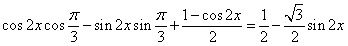
所以函數(shù)f(x)的最大值為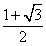 ,最小正周期
,最小正周期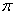 .
. 

(2)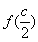 =
=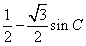 =-
=-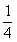 ,
所以
,
所以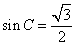 ,
因為C為銳角, 所以
,
因為C為銳角, 所以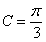 ,
,
又因為在 ABC 中, cosB=
ABC 中, cosB=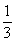 , 所以
, 所以
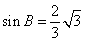 ,
所以
,
所以 

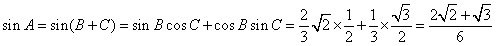 .
.
[命題立意]:本題主要考查三角函數(shù)中兩角和差的弦函數(shù)公式、二倍角公式、三角函數(shù)的性質以及三角形中的三角關系.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com