
2006學年浙江省五校聯考(一)
數學(理科)試卷
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分.卷面共150分,考試時間120分鐘.
第Ⅰ卷(選擇題 共50分)
一、選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1、已知集合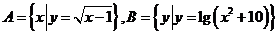 ,則有( )
,則有( )
(A)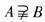 (B)
(B)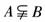 (C)
(C) (D)A=CRB
(D)A=CRB
2、如果復數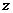 滿足:
滿足: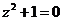 ,則
,則 (
(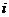 為虛數單位)的值為( )
為虛數單位)的值為( )
(A)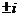 (B)
(B)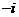 (C)
(C)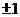 (D)1
(D)1
3、已知隨機變量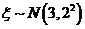 ,若
,若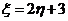 ,則
,則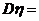 ( )
( )
(A)0 (B)1 (C)2 (D)4
4、已知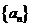 是正項的等差數列,如果滿足:
是正項的等差數列,如果滿足: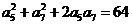 ,則數列
,則數列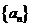 的前11項的和為( )
的前11項的和為( )
(A)8 (B)44 (C)56 (D)64
5、函數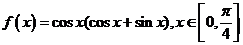 的值域是( )
的值域是( )
(A)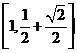 (B)
(B)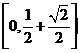 (C)
(C)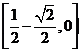 (D)
(D)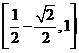
6、設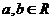 ,則“
,則“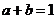 ”是“
”是“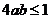 ”的( )條件
”的( )條件
(A)充分非必要 (B)必要非充分 (C)充分必要 (D)既不充分也不必要
7、函數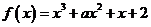 在
在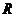 上存在極值點,則實數
上存在極值點,則實數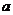 的取值范圍是( )
的取值范圍是( )
(A)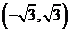 (B)
(B)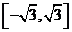
(C)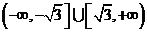 (D)
(D)
8、同時拋擲三枚骰子,出現正面朝上的點數之和不大于5的概率是( )
(A)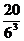 (B)
(B)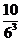 (C)
(C)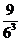 (D)
(D)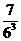
9、已知平面向量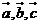 滿足
滿足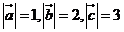 ,且向量
,且向量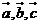 兩兩所成的角相等,則
兩兩所成的角相等,則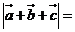 ( )
( )
(A)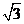 (B)
(B) 或
或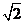 (C)6
(D)
(C)6
(D) 或
或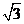
10、設二次函數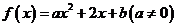 ,若方程
,若方程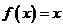 無實數解,則方程
無實數解,則方程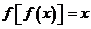 的實數根的個數為( )
的實數根的個數為( )
(A)0 (B)2 (C)4 (D)4個以上
第Ⅱ卷(非選擇題,共100分)
二、填空題:本大題共4小題,每小題4分,共16分.
11、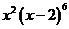 展開式中
展開式中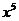 的系數是 ▲ .
的系數是 ▲ .
12、用0,1,2,3,4這五個數字組成無重復數字的五位數,其中恰有一個偶數夾在兩個奇數之間的五位數的個數是 ▲ (用數字作答).
13、在直角三角形ABC中,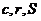 分別表示它的斜邊、內切圓半徑和面積,則
分別表示它的斜邊、內切圓半徑和面積,則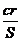 的最小值是 ▲ .
的最小值是 ▲ .
14、命題:①若函數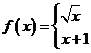
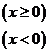 ,則
,則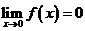 ;②若
;②若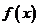 在
在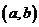 內連續,則
內連續,則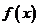 在
在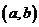 內一定存在最大值和最小值;③已知
內一定存在最大值和最小值;③已知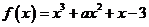 ,若
,若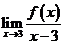 存在,則
存在,則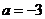 ;④
;④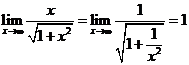 .則其中不正確的命題的序號是
▲ .
.則其中不正確的命題的序號是
▲ .
三、解答題:本大題共6小題,每小題14分,共84分.
15.(本小題滿分14分)已知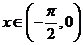 ,
,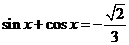 .
.
(1)求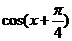 的值;
的值;
(2)求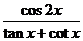 的值.
的值.
16.(本小題滿分14分)已知函數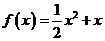 ,
,
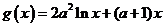 .
.
(1)求過點 與曲線
與曲線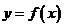 相切的切線方程;
相切的切線方程;
(2)如果函數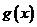 在定義域內存在導數為零的點,求實數
在定義域內存在導數為零的點,求實數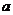 的取值范圍;
的取值范圍;
(3)設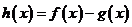 ,求函數
,求函數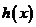 的單調遞增區間.
的單調遞增區間.
17.(本小題滿分14分)
在一袋中有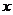 個紅球、3個黑球和2個白球,現從中任取3個.
個紅球、3個黑球和2個白球,現從中任取3個.
(1)如果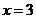 ,求取出的3球中顏色都相同的概率;
,求取出的3球中顏色都相同的概率;
(2)在(1)的前提下,設 表示取出的3球中紅球的個數,求
表示取出的3球中紅球的個數,求 的概率分布及數學期望
的概率分布及數學期望
(3)如果取出的3球的顏色各不相同的概率為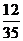 ,求
,求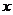 的值.
的值.
18.(本小題滿分14分)已知正項數列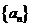 滿足:
滿足:
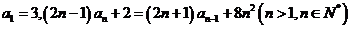 .
.
(1)求證:數列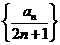 是等差數列;
是等差數列;
(2)求數列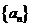 的通項
的通項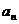 ;
;
(3)求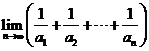 的值.
的值.
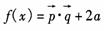 19.(本小題滿分14分)已知向量
19.(本小題滿分14分)已知向量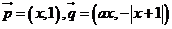 ,設
,設
(1)若 ,求證:函數
,求證:函數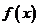 的值恒正;
的值恒正;
(2)如果不等式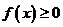 對一切實數
對一切實數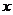 恒成立,求實數
恒成立,求實數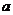 的取值范圍.
的取值范圍.
20.(本小題滿分14分)設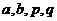 都是正實數,且
都是正實數,且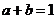 ,定義函數
,定義函數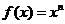
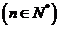 .
.
(1)試比較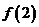 與
與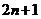 的大小;
的大小;
(2)證明: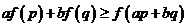 .
.
2006學年浙江省五校聯考(一)
數學(理科)答題卷
試題
一
二
三
總分
15
16
17
18
19
20
得分
卷Ⅰ(選擇題,共50分)
題目
1
2
3
4
5
6
7
8
9
10
卷Ⅱ(非選擇題,共100分)
二、填空題:本大題共4小題,每小題4分,共16分.
11. 12.
13. 14.
三、解答題:本大題共6小題,每小題14分,共84分.
15.(本小題滿分14分)已知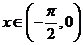 ,
,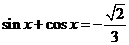 .
.
(1)求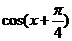 的值;
的值;
(2)求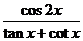 的值.
的值.
16.(本小題滿分14分)已知函數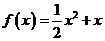 ,
,
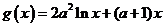 .
.
(1)求過點 與曲線
與曲線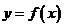 相切的切線方程;
相切的切線方程;
(2)如果函數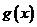 在定義域內存在導數為零的點,求實數
在定義域內存在導數為零的點,求實數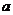 的取值范圍;
的取值范圍;
(3)設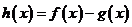 ,求函數
,求函數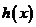 的單調遞增區間
的單調遞增區間
17.(本小題滿分14分)
在一袋中有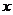 個紅球、3個黑球和2個白球,現從中任取3個.
個紅球、3個黑球和2個白球,現從中任取3個.
(1)如果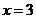 ,求取出的3球中顏色都相同的概率;
,求取出的3球中顏色都相同的概率;
(2)在(1)的前提下,設 表示取出的3球中紅球的個數,求
表示取出的3球中紅球的個數,求 的概率分布及數學期望
的概率分布及數學期望
(3)如果取出的3球的顏色各不相同的概率為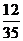 ,求
,求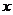 的值.
的值.
18.(本小題滿分14分)已知正項數列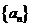 滿足:
滿足:
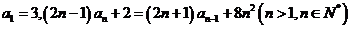 .
.
(1)求證:數列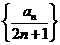 是等差數列;
是等差數列;
(2)求數列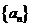 的通項
的通項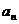 ;
;
(3)求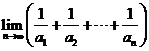 的值.
的值.
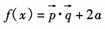 19.(本小題滿分14分)已知向量
19.(本小題滿分14分)已知向量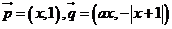 ,設(1)若
,設(1)若 ,求證:函數
,求證:函數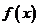 的值恒正;
的值恒正;
(2)如果不等式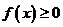 對一切實數
對一切實數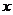 恒成立,求實數
恒成立,求實數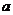 的取值范圍.
的取值范圍.
20.(本小題滿分14分)設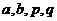 都是正實數,且
都是正實數,且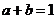 ,定義函數
,定義函數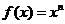
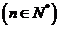 .
.
(1)試比較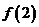 與
與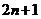 的大小;
的大小;
(2)證明: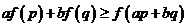 .
.
浙江省2006學年高三五校聯考數學卷(理科)評分參考
題號
1
2
3
4
5
6
7
8
9
10
答案
C
C
B
B
A
A
D
B
D
A
二.填空題:
11. 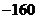 12.28 13.
12.28 13.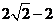 14.①②④
14.①②④
三.解答題:
15.(1)∵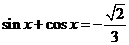 ,∴
,∴ 2分
2分
∵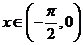 ,∴
,∴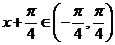 ,
4分
,
4分
∴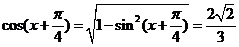 .
.
(2)∵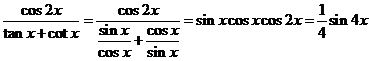 8分
8分
又∵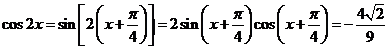 10分
10分
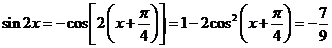 12分
12分
∴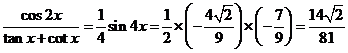 14分
14分
16.(1) ,∵點
,∵點 在曲線上,∴
在曲線上,∴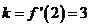
∴所求的切線方程為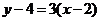 ,即
,即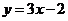 3分
3分
(2)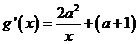
若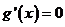 ,則
,則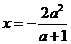 .
.
∵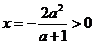 ,∴
,∴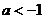 .
6分
.
6分
(3)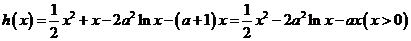
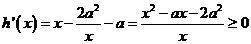
即 11分
11分
當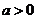 時,單調遞增區間為
時,單調遞增區間為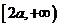
當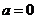 時,單調遞增區間為
時,單調遞增區間為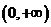
當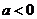 時,單調遞增區間為
時,單調遞增區間為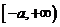 14分
14分
17.(1)設3球中顏色都相同的事件為A
當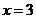 時,
時,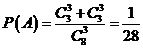 4分
4分
(2)

0
1
2
3

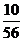
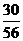
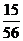
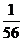
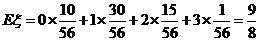 9分
9分
(3)設取出3球中顏色都不相同的事件為B,則有
 11分
11分
依題意有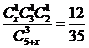
化簡得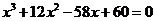 12分
12分
即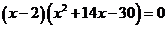
因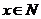 ,所以
,所以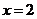 14分
14分
18.(1)∵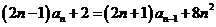
∴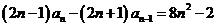
即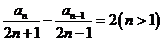 4分
4分
∵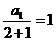 ,∴
,∴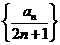 是以1為首項,2為公差的等差數列 5分
是以1為首項,2為公差的等差數列 5分
(2)∵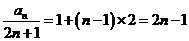
∴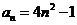 9分
9分
(3)∵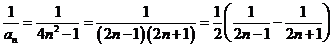 11分
11分
∴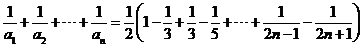 12分
12分
∴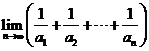
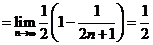 14分
14分
19.(1)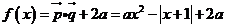 1分
1分
∵ ,∴
,∴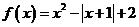
當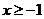 時,
時,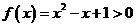 恒成立
3分
恒成立
3分
當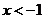 時,
時,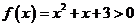 恒成立
5分
恒成立
5分
∴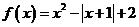 對一切
對一切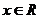 都恒正.
6分
都恒正.
6分
(2)方法1:因為對一切實數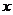 ,都有
,都有
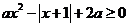
即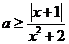 8分
8分
設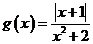 ,則
,則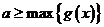 9分
9分
令 ,則
,則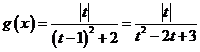
(?)當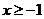 ,即
,即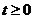 時,有
時,有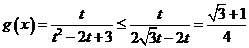
當且僅當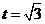 ,即
,即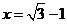 時,等號成立.
11分
時,等號成立.
11分
(?)當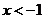 ,即
,即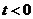 時,有
時,有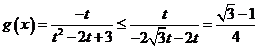
當且僅當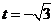 ,即
,即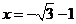 時,等號成立.
13分
時,等號成立.
13分
綜合可得 ,所以實數
,所以實數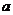 的取值范圍是
的取值范圍是 14分
14分
方法2:把問題轉化為不等式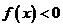 的解集為空集
的解集為空集
即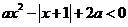 7分
7分
當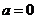 ,則
,則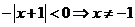 ,矛盾
8分
,矛盾
8分
當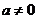 時,不等式
時,不等式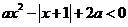 要無解
要無解
(?)當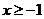 時,
時,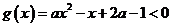 無解
無解
若 時,則
時,則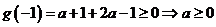 矛盾
矛盾
若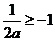 時,則
時,則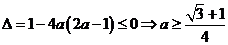 或
或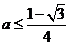
則有 (1)
11分
(1)
11分
(?)當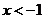 ,
,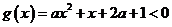 無解
無解
若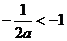 時,
時,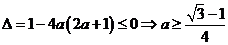 或
或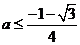
則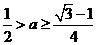
若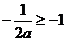 時,則
時,則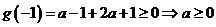
則
綜合有 (2)
13分
(2)
13分
所以實數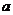 的取值范圍是
的取值范圍是 14分
14分
20.(1)當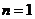 時,
時,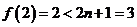 1分
1分
當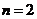 時,
時,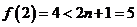 2分
2分
當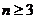 時,
時,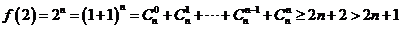
(用數學歸納法也可以證明). 6分
(2)即證: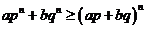 7分
7分
證法1:(數學歸納法)
(?)當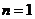 時,
時,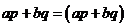 不等式成立,
8分
不等式成立,
8分
(?)假設 時,有
時,有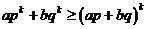
當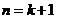 時,
時,
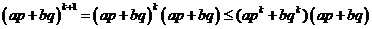
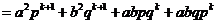
因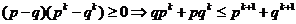
故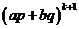
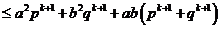
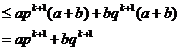
即當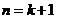 時命題成立.
13分
時命題成立.
13分
根據(?)(?)可得對一切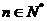 不等式均成立.
14分
不等式均成立.
14分
方法2:構造函數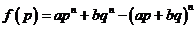
若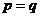 ,則等號成立,
7分
,則等號成立,
7分
若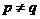 ,根據對稱性,不妨設
,根據對稱性,不妨設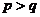 ,當
,當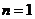 時,不等式成立,
8分
時,不等式成立,
8分
當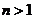 時,
時,
因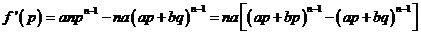 10分
10分
∵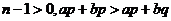
∴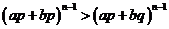
∴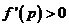 ,即
,即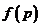 在
在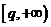 上是單調增函數
12分
上是單調增函數
12分
當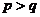 時,有
時,有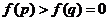
∴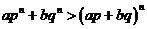
綜上得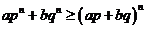 即
即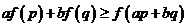 .
14分
.
14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com