
19、(廣東省北江中學2009屆高三上學期12月月考)旅游公司為3個旅游團提供4條旅游線路,每個旅游團任選其中一條.
(Ⅰ)求3個旅游團選擇3條不同的線路的概率;
(Ⅱ)求選擇甲線路旅游團數的分布列和期望.
解:(1)3個旅游團選擇3條不同線路的概率為:P1=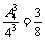 ……4分
……4分
(2)設選擇甲線路旅游團數為ξ,則ξ=0,1,2,3………………5分
P(ξ=0)=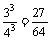 P(ξ=1)=
P(ξ=1)=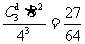
P(ξ=2)= 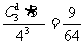 P(ξ=3)=
P(ξ=3)= 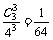 ………………9分
………………9分
∴ξ的分布列為:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
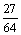 |
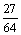 |
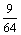 |
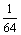
|
………………10分
∴期望Eξ=0×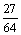 +1×
+1×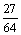 +2×
+2×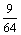 +3×
+3×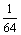 =
=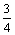 ………………12分
………………12分
18、(江蘇省常州市2008-2009高三第一學期期中統一測試數學試題)一個盒子裝有六張卡片,上面分別寫著如下六個定義域為R的函數:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)現從盒子中任取兩張卡片,將卡片上的函數相加得一個新函數,求所得函數是奇函數的概率;
(2)現從盒子中進行逐一抽取卡片,且每次取出后均不放回,若取到一張記有偶函數的卡片則停止抽取,否則繼續進行,求抽取次數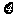 的分布列和數學期望.
的分布列和數學期望.
解:(1)記事件A為“任取兩張卡片,將卡片上的函數相加得到的函數是奇函數”,由題意知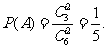 4′
4′
(2)ξ可取1,2,3,4.
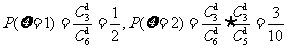 ,
,
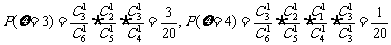 ; 8′
; 8′
故ξ的分布列為
|
ξ |
1 |
2 |
3 |
4 |
|
P |
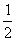 |
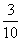 |
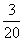 |
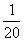 |

答:ξ的數學期望為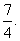 10′
10′
17、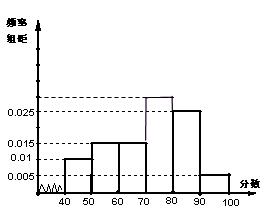 (江蘇省常州市2008-2009高三第一學期期中統一測試數學試題)某校從參加高一年級期末考試的學生中抽出60名學生,將其成績(是不小于40不大于100的整數)分成六段
(江蘇省常州市2008-2009高三第一學期期中統一測試數學試題)某校從參加高一年級期末考試的學生中抽出60名學生,將其成績(是不小于40不大于100的整數)分成六段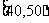 ,
,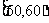 …
…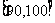 后畫出如下部分
后畫出如下部分
(1)求第四小組的頻率,并補全這個頻率分布直方圖.
(2) 觀察頻率分布直方圖圖形的信息,估計這次考試的及格率(60分及以上為及格)和平均分.
解:(1)因為各組的頻率和等于1,故第四組的頻率:
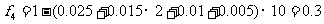 3′
3′
直方圖如右所示 6′
(2)依題意,60及以上的分數所在的第三、四、五、六組,
頻率和為
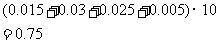
所以,抽樣學生成績的合格率是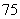 %..
9 ′
%..
9 ′
利用組中值估算抽樣學生的平均分
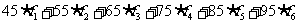
=
=71
估計這次考試的平均分是71分 12′
16、(四川省成都市高中數學2009級九校聯考)在一次籃球練習課中,規定每人投籃5次,若投中2次就稱為“通過”若投中3次就稱為“優秀”并停止投籃。已知甲每次投籃投中概率是。
(1)求甲恰好投籃3次就“通過”的概率;
(2)設甲投中籃的次數為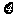 ,求隨機變量
,求隨機變量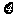 的分布列及期望
的分布列及期望 。
。
解:①前2次中恰有一次投中且第3次也投中,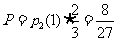 …………5分
…………5分
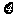 |
0 |
1 |
2 |
3 |
|
p |
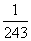 |
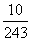 |
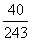 |
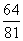 |
②
……………………………………5分
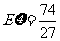 …………………………2分
…………………………2分
15、(四川省成都市高中數學2009級九校聯考)某單位組織4個部門的職工旅游,規定每個部門只能在峨眉山、泰山、華山3個景區中任選一個,假設各部門選擇每個景區是等可能的.
(Ⅰ)求3個景區都有部門選擇的概率;
(Ⅱ)求恰有2個景區有部門選擇的概率.
解:某單位的4個部門選擇3個景區可能出現的結果數為34.由于是任意選擇,這些結果出現的可能性都相等.
(I)3個景區都有部門選擇可能出現的結果數為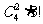 (從4個部門中任選2個作為1組,另外2個部門各作為1組,共3組,共有
(從4個部門中任選2個作為1組,另外2個部門各作為1組,共3組,共有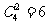 種分法,每組選擇不同的景區,共有3!種選法),記“3個景區都有部門選擇”為事件A1,那么事件A1的概率為
種分法,每組選擇不同的景區,共有3!種選法),記“3個景區都有部門選擇”為事件A1,那么事件A1的概率為
P(A1)=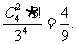 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
(II)解法一:分別記“恰有2個景區有部門選擇”和“4個部門都選擇同一個景區”為事件A2和A3,則事件A3的概率為P(A3)=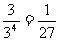 ,事件A2的概率為
,事件A2的概率為
P(A2)=1-P(A1)-P(A3)=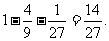 。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。6分
14、(2009屆福建省福鼎一中高三理科數學強化訓練綜合卷一)下表為某班英語及數學成績的分布.學生共有50人,成績分1~5五個檔次.例如表中所示英語成績為4分、數學成績為2分的學生為5人.將全班學生的姓名卡片混在一起,任取一枚,該卡片同學的英語成績為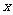 ,數學成績為
,數學成績為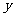 。設
。設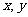 為隨機變量(注:沒有相同姓名的學生)
為隨機變量(注:沒有相同姓名的學生)
 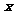 |
數學 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英語 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
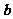 |
6 |
0 |
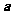 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
(1)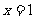 的概率為多少?
的概率為多少?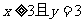 的概率為多少?
的概率為多少?
(2) (理)  等于多少?若
等于多少?若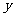 的期望為
的期望為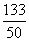 ,試確定
,試確定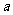 ,
, 的值 .
的值 .
解:(1)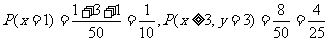 ;6分
(2)(理)
;6分
(2)(理)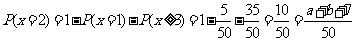
 ①;---------9分
又
①;---------9分
又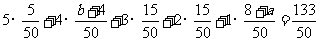
 ②; - --------11分
②; - --------11分
結合①②可得 ,
,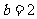 .
---------12分
.
---------12分
13、(重慶市大足中學2009年高考數學模擬試題)甲、乙兩個箱子中裝有大小相同的小球,甲箱中有2個紅球和2個黑球,乙箱中裝有2個黑球和3個紅球,現從甲箱和乙箱中各取一個小球并且交換。
(1)求交換后甲箱中剛好有兩個黑球的概率。(6分)
(2)設交換后甲箱中黑球的個數為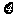 ,
,
求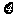 的分布列和數學期望。(6分)
的分布列和數學期望。(6分)

12、(天津市漢沽一中2008~2009學年度高三第四次月考試題)將一個半徑適當的小球放入如圖所示的容器最上方的入口處,小球將自由下落.小球在下落過程中,將3次遇到黑色障礙物,最后落入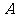 袋或
袋或 袋中.已知小球每次遇到黑色障礙物時向左、右兩邊下落的概率都是.
袋中.已知小球每次遇到黑色障礙物時向左、右兩邊下落的概率都是.
 (Ⅰ)求小球落入
(Ⅰ)求小球落入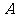 袋中的概率
袋中的概率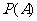 ;
;
(Ⅱ)在容器入口處依次放入4個小球,記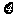 為落入
為落入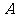
袋中小球的個數,試求 的概率和
的概率和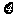 的數學期望
的數學期望 .
.
解: (Ⅰ)解法一:記小球落入 袋中的概率
袋中的概率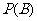 ,則
,則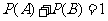 ,
,
由于小球每次遇到黑色障礙物時一直向左或者一直向右下落,小球將落入 袋,所以
袋,所以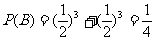 ‘………………………………………………………………… 2分
‘………………………………………………………………… 2分
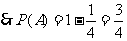 . ……………………………………………………………… 5分
. ……………………………………………………………… 5分
解法二:由于小球每次遇到黑色障礙物時,有一次向左和兩次向右或兩次向左和一次向右下落時小球將落入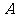 袋.
袋.
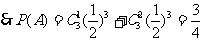 ,
……………………………… 5分
,
……………………………… 5分
(Ⅱ)由題意,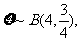 所以有 ……………………………………………… 7分
所以有 ……………………………………………… 7分
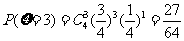 ,
……………………………………… 10分
,
……………………………………… 10分
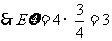 .
………………………………
12分
.
………………………………
12分
11、(遼寧省大連市第二十四中學2009屆高三高考模擬)有一種舞臺燈,外形是正六棱柱ABCDEF-A1B1C1D1E1F1,在其每一個側面上(不在棱上)安裝5只顏色各異的彩燈,假若每只燈正常發光的概率是0.5,若一個面上至少有3只燈發光,則不需要維修,否則需要更換這個面. 假定更換一個面需100元,用ξ表示維修一次的費用.
(1)求面ABB1A1需要維修的概率;
(2)寫出ξ的分布列,并求ξ的數學期望.
解:(1)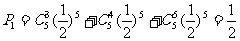 …………………………6分
…………………………6分
(2)因為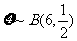
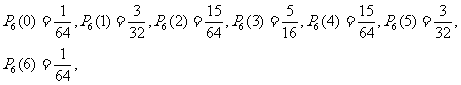
|
ξ |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
|
P |
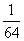 |
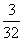 |
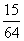 |
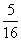 |
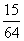 |
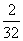 |
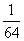 |
………………………………………………10分
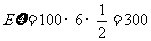 (元)………………………………………………12分
(元)………………………………………………12分
10、(湖南省衡陽市八中2009屆高三第三次月考試題)2008年中國北京奧運會吉祥物由5個“中國福娃”組成,分別叫貝貝、晶晶、歡歡、迎迎、妮妮。現有8個相同的盒子,每個盒子中放一只福娃,每種福娃的數量如下表:
|
福娃名稱 |
貝貝 |
晶晶 |
歡歡 |
迎迎 |
妮妮 |
|
數量 |
1 |
2 |
3 |
1 |
1 |
從中隨機地選取5只。
(1)求選取的5只恰好組成完整“奧運吉祥物”的概率;
(2)若完整地選取奧運會吉祥物記100分;若選出的5只中僅差一種記80分;差兩種記60分;以此類推。設ξ表示所得的分數,求ξ的分布列和期望值。
解:(1)選取的5只恰好組成完整“奧運吉祥物”的概率
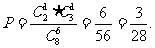
(2)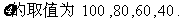
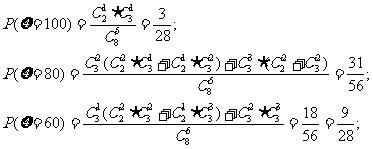
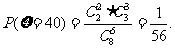 ξ的分布列為:
ξ的分布列為:
|
ξ |
100 |
80 |
60 |
40 |
|
P |
 |
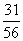 |
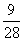 |
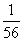 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com