
7.對數不等式
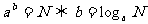
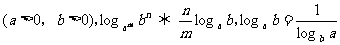

(1)當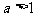 時,
時,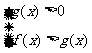 ;(2)當
;(2)當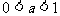 時,
時, 。
。
課前預習
6.指數不等式
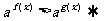
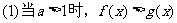 ;
;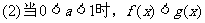 ;
;
5.簡單的絕對值不等式
①討論法:討論絕對值中的式于大于零還是小于零,然后去掉絕對值符號,轉化為一般不等式;
②等價變形:
|f(x)|<g(x)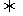 -g(x)<f(x)<g(x),
-g(x)<f(x)<g(x),
|f(x)|>g(x)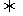 f(x)>g (x)或f(x)<g(x)。
f(x)>g (x)或f(x)<g(x)。
4.分式不等式
分式不等式的等價變形: >0
>0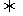 f(x)·g(x)>0,
f(x)·g(x)>0, ≥0
≥0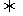
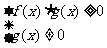 。
。
3.一元二次不等式
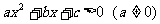 或
或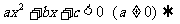 分
分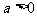 及
及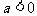 情況分別解之,還要注意
情況分別解之,還要注意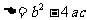 的三種情況,即
的三種情況,即 或
或 或
或 ,最好聯系二次函數的圖象。
,最好聯系二次函數的圖象。
2.一元一次不等式
 情況分別解之。
情況分別解之。
解不等式是求定義域、值域、參數的取值范圍時的重要手段,與“等式變形”并列的“不等式的變形”,是研究數學的基本手段之一。
高考試題中,對解不等式有較高的要求,近兩年不等式知識占相當大的比例。
1.不等式同解變形
(1)同解不等式((1) 與
與 同解;
同解;
(2)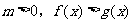 與
與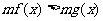 同解,
同解,
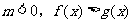 與
與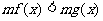 同解;
同解;
(3)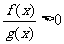 與
與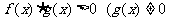 同解);
同解);
3.分析法
證明不等式時,有時可以從求證的不等式出發,分析使這個不等式成立的充分條件,把證明不等式轉化為判定這些充分條件是否具備的問題,如果能夠肯定這些充分條件都已具備,那么就可以斷定原不等式成立,這種方法通常叫做分析法。
2.綜合法
利用某些已經證明過的不等式(例如算術平均數與幾何平均數的定理)和不等式的性質,推導出所要證明的不等式,這個證明方法叫綜合法;
1.比較法
比較法證明不等式的一般步驟:作差-變形-判斷-結論;為了判斷作差后的符號,有時要把這個差變形為一個常數,或者變形為一個常數與一個或幾個平方和的形式,也可變形為幾個因式的積的形式,以便判斷其正負。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com