
114.證明平面與平面的垂直的思考途徑
(1)轉化為判斷二面角是直二面角;
(2)轉化為線面垂直.
113.證明直線與平面垂直的思考途徑
(1)轉化為該直線與平面內任一直線垂直;
(2)轉化為該直線與平面內相交二直線垂直;
(3)轉化為該直線與平面的一條垂線平行;
(4)轉化為該直線垂直于另一個平行平面;
(5)轉化為該直線與兩個垂直平面的交線垂直.
112.證明直線與直線的垂直的思考途徑
(1)轉化為相交垂直;
(2)轉化為線面垂直;
(3)轉化為線與另一線的射影垂直;
(4)轉化為線與形成射影的斜線垂直.
111.證明平面與平面平行的思考途徑
(1)轉化為判定二平面無公共點;
(2)轉化為線面平行;
(3)轉化為線面垂直.
110.證明直線與平面的平行的思考途徑
(1)轉化為直線與平面無公共點;
(2)轉化為線線平行;
(3)轉化為面面平行.
109.證明直線與直線的平行的思考途徑
(1)轉化為判定共面二直線無交點;
(2)轉化為二直線同與第三條直線平行;
(3)轉化為線面平行;
(4)轉化為線面垂直;
(5)轉化為面面平行.
91.圓的切線方程
(1)已知圓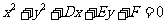 .
.
①若已知切點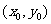 在圓上,則切線只有一條,其方程是
在圓上,則切線只有一條,其方程是
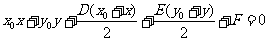 .
.
當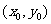 圓外時,
圓外時, 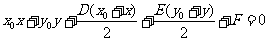 表示過兩個切點的切點弦方程.
表示過兩個切點的切點弦方程.
②過圓外一點的切線方程可設為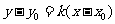 ,再利用相切條件求k,這時必有兩條切線,注意不要漏掉平行于y軸的切線.
,再利用相切條件求k,這時必有兩條切線,注意不要漏掉平行于y軸的切線.
③斜率為k的切線方程可設為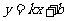 ,再利用相切條件求b,必有兩條切線.
,再利用相切條件求b,必有兩條切線.
(2)已知圓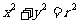 .
.
①過圓上的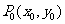 點的切線方程為
點的切線方程為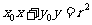 ;
;
②斜率為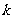 的圓的切線方程為
的圓的切線方程為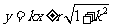 .
.
橢圓
l
橢圓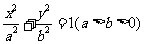 的參數方程是
的參數方程是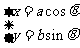 .
.
l
橢圓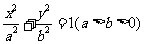 焦半徑公式
焦半徑公式
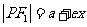 ,
,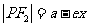 ,
,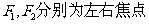
l
焦點三角形:P為橢圓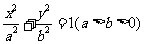 上一點,則三角形
上一點,則三角形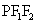 的面積S=
的面積S=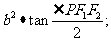 特別地,若
特別地,若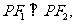 此三角形面積為
此三角形面積為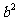 ;
;
l
在橢圓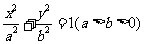 上存在點P,使
上存在點P,使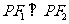 的條件是c≥b,即橢圓的離心率e的范圍是
的條件是c≥b,即橢圓的離心率e的范圍是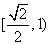 ;
;
l 橢圓的的內外部
(1)點 在橢圓
在橢圓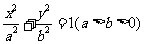 的內部
的內部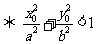 .
.
(2)點 在橢圓
在橢圓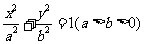 的外部
的外部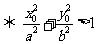 .
.
l 橢圓的切線方程
(1)橢圓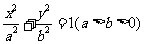 上一點
上一點 處的切線方程是
處的切線方程是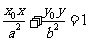 .
.
(2)過橢圓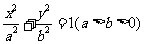 外一點
外一點 所引兩條切線的切點弦方程是
所引兩條切線的切點弦方程是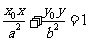 .
.
(3)橢圓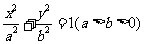 與直線
與直線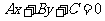 相切的條件是
相切的條件是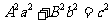 .雙曲線
.雙曲線
l
雙曲線 的焦半徑公式
的焦半徑公式
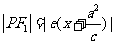 ,
,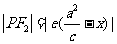 .
.
l 雙曲線的內外部
(1)點 在雙曲線
在雙曲線 的內部
的內部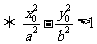 .
.
(2)點 在雙曲線
在雙曲線 的外部
的外部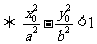 .
.
l 雙曲線的方程與漸近線方程的關系
(1)若雙曲線方程為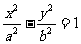
 漸近線方程:
漸近線方程: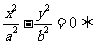
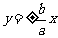 .
.
(2)若漸近線方程為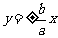
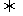
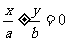
 雙曲線可設為
雙曲線可設為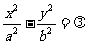 .
.
(3)若雙曲線與 有公共漸近線,可設為
有公共漸近線,可設為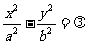 (
(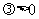 ,焦點在x軸上,
,焦點在x軸上,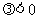 ,焦點在y軸上).
,焦點在y軸上).
l 雙曲線的切線方程
(1)雙曲線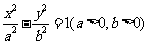 上一點
上一點 處的切線方程是
處的切線方程是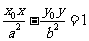 .
.
(2)過雙曲線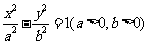 外一點
外一點 所引兩條切線的切點弦方程是
所引兩條切線的切點弦方程是
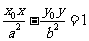 .
.
(3)雙曲線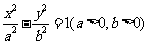 與直線
與直線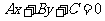 相切的條件是
相切的條件是 .
.
l 焦點到漸近線的距離等于虛半軸的長度(即b值)
拋物線
l 焦點與半徑

l 焦半徑公式
拋物線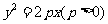 ,C
,C 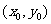 為拋物線上一點,焦半徑
為拋物線上一點,焦半徑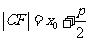 .
.
過焦點弦長 .對焦點在y軸上的拋物線有類似結論。
.對焦點在y軸上的拋物線有類似結論。
l 設點方法
拋物線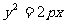 上的動點可設為P
上的動點可設為P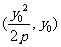 或
或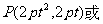 P
P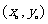 ,其中
,其中
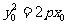 .
.
l 二次函數
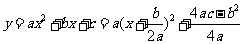
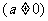 的圖象是拋物線:
的圖象是拋物線:
(1)頂點坐標為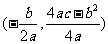 ;
;
(2)焦點的坐標為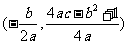 ;
;
(3)準線方程是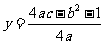 .
.
l 拋物線的內外部
(1)點 在拋物線
在拋物線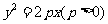 的內部
的內部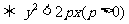 .
.
點 在拋物線
在拋物線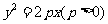 的外部
的外部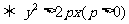 .
.
(2)點 在拋物線
在拋物線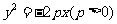 的內部
的內部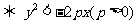 .
.
點 在拋物線
在拋物線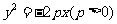 的外部
的外部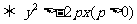 .
.
(3)點 在拋物線
在拋物線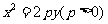 的內部
的內部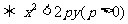 .
.
點 在拋物線
在拋物線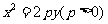 的外部
的外部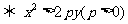 .
.
(4) 點 在拋物線
在拋物線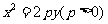 的內部
的內部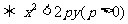 .
.
點 在拋物線
在拋物線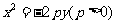 的外部
的外部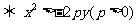 .
.
l 拋物線的切線方程
(1)拋物線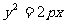 上一點
上一點 處的切線方程是
處的切線方程是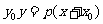 .
.
(2)過拋物線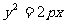 外一點
外一點 所引兩條切線的切點弦方程是
所引兩條切線的切點弦方程是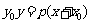 .
.
(3)拋物線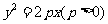 與直線
與直線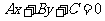 相切的條件是
相切的條件是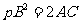 .
.
l
過拋物線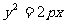 (p>0)的焦點F的直線與拋物線相交于
(p>0)的焦點F的直線與拋物線相交于

圓錐曲線共性問題
l 兩個常見的曲線系方程
(1)過曲線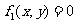 ,
,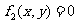 的交點的曲線系方程是
的交點的曲線系方程是
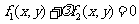 (
(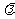 為參數).
為參數).
(2)共焦點的有心圓錐曲線系方程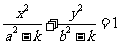 ,其中
,其中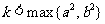 .當
.當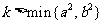 時,表示橢圓; 當
時,表示橢圓; 當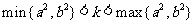 時,表示雙曲線.
時,表示雙曲線.
l 直線與圓錐曲線相交的弦長公式
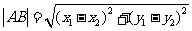 或
或
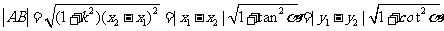
(弦端點A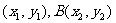
由方程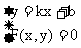 消去y得到
消去y得到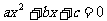 ,
, ,
,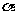 為直線
為直線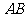 的傾斜角,
的傾斜角,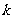 為直線的斜率).
為直線的斜率).
l
涉及到曲線上的 點A,B及線段AB的中點M的關系時,可以利用“點差法:,比如在橢圓中:
l 圓錐曲線的兩類對稱問題
(1)曲線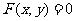 關于點
關于點 成中心對稱的曲線是
成中心對稱的曲線是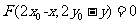 .
.
(2)曲線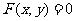 關于直線
關于直線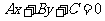 成軸對稱的曲線是
成軸對稱的曲線是
 .
.
l “四線”一方程
對于一般的二次曲線 ,用
,用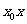 代
代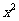 ,用
,用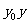 代
代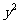 ,用
,用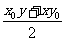 代
代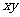 ,用
,用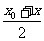 代
代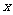 ,用
,用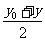 代
代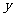 即得方程
即得方程
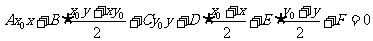 ,曲線的切線,切點弦,中點弦,弦中點方程均是此方程得到.立體幾何
,曲線的切線,切點弦,中點弦,弦中點方程均是此方程得到.立體幾何
85. 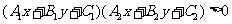 或
或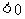 所表示的平面區域
所表示的平面區域
設曲線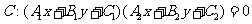 (
(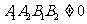 ),則
),則
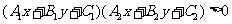 或
或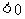 所表示的平面區域是:
所表示的平面區域是:
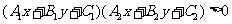 所表示的平面區域上下兩部分;
所表示的平面區域上下兩部分;
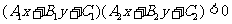 所表示的平面區域上下兩部分.圓
所表示的平面區域上下兩部分.圓
l 圓的四種方程
(1)圓的標準方程 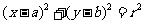 .
.
(2)圓的一般方程 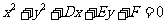 (
(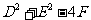 >0).
>0).
(3)圓的參數方程  .
.
(4)圓的直徑式方程 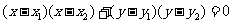 (圓的直徑的端點是
(圓的直徑的端點是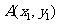 、
、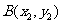 ).
).
l 圓系方程
(1)過點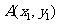 ,
,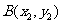 的圓系方程是
的圓系方程是
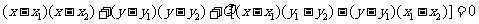
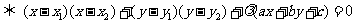 ,其中
,其中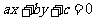 是直線
是直線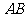 的方程,λ是待定的系數.
的方程,λ是待定的系數.
(2)過直線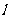 :
: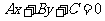 與圓
與圓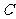 :
: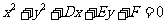 的交點的圓系方程是
的交點的圓系方程是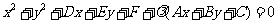 ,λ是待定的系數.
,λ是待定的系數.
(3) 過圓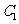 :
: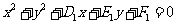 與圓
與圓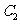 :
: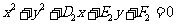 的交點的圓系方程是
的交點的圓系方程是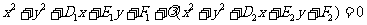 ,λ是待定的系數.
,λ是待定的系數.
l 點與圓的位置關系
點 與圓
與圓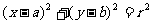 的位置關系有三種
的位置關系有三種
若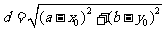 ,則
,則
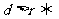 點
點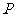 在圓外;
在圓外;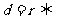 點
點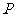 在圓上;
在圓上;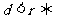 點
點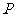 在圓內.
在圓內.
l 直線與圓的位置關系
直線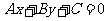 與圓
與圓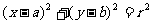 的位置關系有三種:
的位置關系有三種:
 ;
;
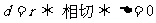 ;
;
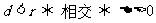 .
.
其中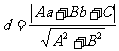 .
.
l 兩圓位置關系的判定方法
設兩圓圓心分別為O1,O2,半徑分別為r1,r2,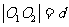
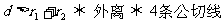 ;
;
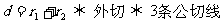 ;
;
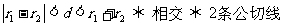 ;
;
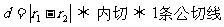 ;
;
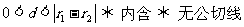 .
.
75.無理不等式
(1)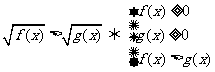 .
.
(2)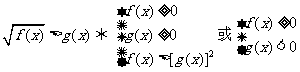 .
.
(3)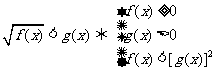 .
.
l 指數不等式與對數不等式
(1)當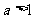 時,
時,
 ;
;
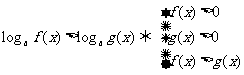 .
.
(2)當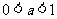 時,
時,
 ;
;
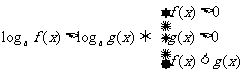
直線方程
l 斜率公式
①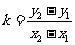 (
(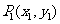 、
、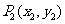 ).② k=tanα(α為直線傾斜角)
).② k=tanα(α為直線傾斜角)
l 直線的五種方程
(1)點斜式 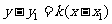 (直線
(直線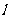 過點
過點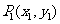 ,且斜率為
,且斜率為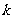 ).
).
(2)斜截式 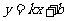 (b為直線
(b為直線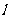 在y軸上的截距).
在y軸上的截距).
(3)兩點式 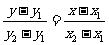 (
(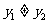 )(
)(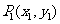 、
、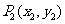 (
(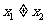 )).
)).
(4)截距式 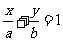 (
( 分別為直線的橫、縱截距,
分別為直線的橫、縱截距, )
)
(5)一般式 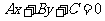 (其中A、B不同時為0).
(其中A、B不同時為0).
l 兩條直線的平行和垂直
(1)若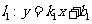 ,
,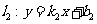
①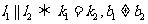 ;
;
②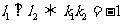 .
.
(2)若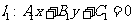 ,
,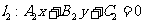 ,且A1、A2、B1、B2都不為零,
,且A1、A2、B1、B2都不為零,
①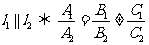 ;
;
②兩直線垂直的充要條件是 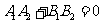 ;即:
;即: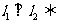
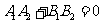
l 夾角公式
(1)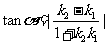 .
.
(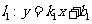 ,
,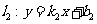 ,
,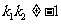 )
)
(2)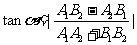 .
.
(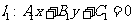 ,
,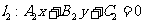 ,
,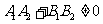 ).
).
直線 時,直線l1與l2的夾角是
時,直線l1與l2的夾角是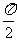 .
.
l
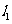 到
到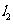 的角公式
的角公式
(1)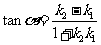 .
.
(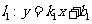 ,
,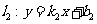 ,
,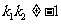 )
)
(2)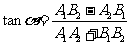 .
.
(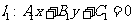 ,
,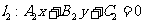 ,
,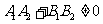 ).
).
直線 時,直線l1到l2的角是
時,直線l1到l2的角是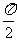 .
.
l 四種常用直線系方程
(1)定點直線系方程:經過定點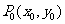 的直線系方程為
的直線系方程為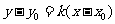 (除直線
(除直線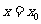 ),其中
),其中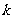 是待定的系數; 經過定點
是待定的系數; 經過定點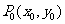 的直線系方程為
的直線系方程為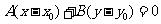 ,其中
,其中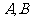 是待定的系數.
是待定的系數.
(2)共點直線系方程:經過兩直線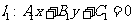 ,
,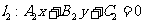 的交點的直線系方程為
的交點的直線系方程為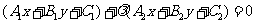 (除
(除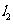 ),其中λ是待定的系數.
),其中λ是待定的系數.
(3)平行直線系方程:直線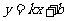 中當斜率k一定而b變動時,表示平行直線系方程.與直線
中當斜率k一定而b變動時,表示平行直線系方程.與直線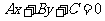 平行的直線系方程是
平行的直線系方程是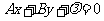 (
(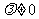 ),λ是參變量.
),λ是參變量.
(4)垂直直線系方程:與直線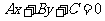 (A≠0,B≠0)垂直的直線系方程是
(A≠0,B≠0)垂直的直線系方程是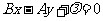 ,λ是參變量.
,λ是參變量.
l 點到直線的距離
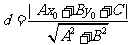 (點
(點 ,直線
,直線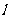 :
: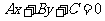 ).
).
l
 或
或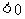 所表示的平面區域
所表示的平面區域
設直線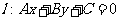 ,若A>0,則在坐標平面內從左至右的區域依次表示
,若A>0,則在坐標平面內從左至右的區域依次表示 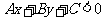 ,
, ,若A<0,則在坐標平面內從左至右的區域依次表示
,若A<0,則在坐標平面內從左至右的區域依次表示  ,
,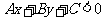 ,可記為“x 為正開口對,X為負背靠背“。(正負指X的系數A,開口對指”<>",背靠背指"><")
,可記為“x 為正開口對,X為負背靠背“。(正負指X的系數A,開口對指”<>",背靠背指"><")
39.數列的同項公式與前n項的和的關系
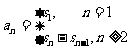 ( 數列
( 數列 的前n項的和為
的前n項的和為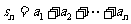 )
)
數列
l
等差數列的通項公式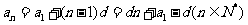 ;
;
其前n項和公式為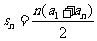
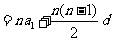
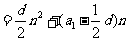 .
.
l
等比數列的通項公式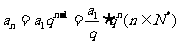 ;
;
其前n項的和公式為
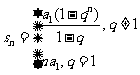 或
或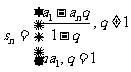 .
.
l
等比差數列 :
: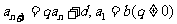 的通項公式為
的通項公式為
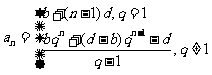 ;
;
其前n項和公式為
 .
.
l 分期付款(按揭貸款)
每次還款 元(貸款
元(貸款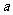 元,
元,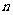 次還清,每期利率為
次還清,每期利率為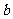 ).
).
三角函數
l 常見三角不等式
(1)若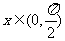 ,則
,則 .(2) 若
.(2) 若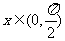 ,則
,則 .
.
(3) 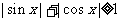 .
.
l 同角三角函數的基本關系式
 ,
,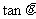 =
=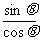 ,
, .
.
l 正弦、余弦的誘導公式

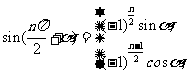

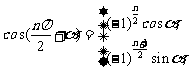
l 和角與差角公式
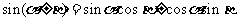 ;
;
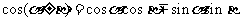 ;
;
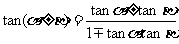 .
.
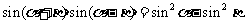 (平方正弦公式);
(平方正弦公式);
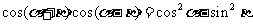 .
.
 =
=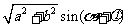 (輔助角
(輔助角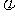 所在象限由點
所在象限由點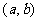 的象限決定,
的象限決定,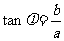 ).
).
l
半角正余切公式: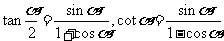
l 二倍角公式
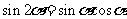 .
.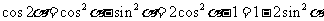 .
.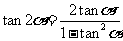 .
.
l 三倍角公式
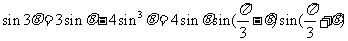 .
.
 .
.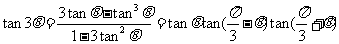 .
.
l 三角函數的周期公式
函數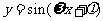 ,x∈R及函數
,x∈R及函數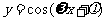 ,x∈R(A,ω,
,x∈R(A,ω,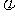 為常數,且A≠0,ω>0)的周期
為常數,且A≠0,ω>0)的周期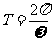 ;函數
;函數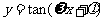 ,
,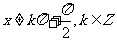 (A,ω,
(A,ω,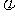 為常數,且A≠0,ω>0)的周期
為常數,且A≠0,ω>0)的周期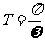 .
.
l
正弦定理 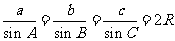 .
.
l 余弦定理
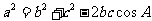 ;
;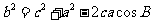 ;
;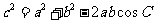 .
.
l 面積定理
(1)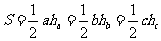 (
(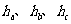 分別表示a、b、c邊上的高).
分別表示a、b、c邊上的高).
(2)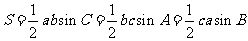 .
.
(3)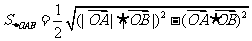 .
.
l 三角形內角和定理
在△ABC中,有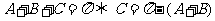
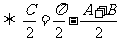
 .
.
l 在三角形中有下列恒等式:
① 
②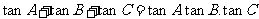
l 簡單的三角方程的通解
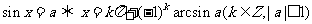 .
.
 .
.
 .
.
特別地,有
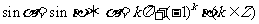 .
.
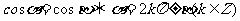 .
.
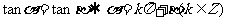 .
.
l 最簡單的三角不等式及其解集
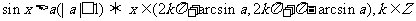 .
.
 .
.
 .
.
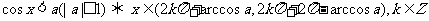 .
.
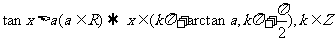 .
.
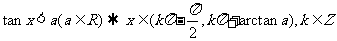 .
.
l
角的變形: 向量
向量
l 實數與向量的積的運算律
設λ、μ為實數,那么
(1) 結合律:λ(μa)=(λμ)a;
(2)第一分配律:(λ+μ)a=λa+μa;(3)第二分配律:λ(a+b)=λa+λb.
l 向量的數量積的運算律:
(1) a·b= b·a (交換律);(2)(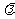 a)·b=
a)·b= 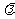 (a·b)=
(a·b)=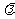 a·b= a·(
a·b= a·(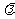 b);
b);
(3)(a+b)·c= a ·c +b·c.
l 平面向量基本定理
如果e1、e 2是同一平面內的兩個不共線向量,那么對于這一平面內的任一向量,有且只有一對實數λ1、λ2,使得a=λ1e1+λ2e2.
不共線的向量e1、e2叫做表示這一平面內所有向量的一組基底.
l 向量平行的坐標表示
設a=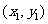 ,b=
,b=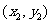 ,且b
,且b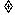 0,則a
0,則a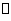 b(b
b(b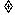 0)
0)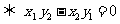 .
.
l a與b的數量積(或內積)
a·b=|a||b|cosθ.
l a·b的幾何意義
數量積a·b等于a的長度|a|與b在a的方向上的投影|b|cosθ的乘積.
l 平面向量的坐標運算
(1)設a=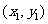 ,b=
,b=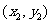 ,則a+b=
,則a+b=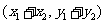 .
.
(2)設a=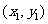 ,b=
,b=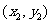 ,則a-b=
,則a-b=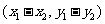 .
.
(3)設A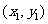 ,B
,B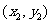 ,則
,則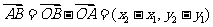 .
.
(4)設a=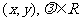 ,則
,則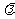 a=
a=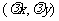 .
.
(5)設a=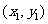 ,b=
,b=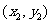 ,則a·b=
,則a·b=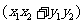 .
.
l 兩向量的夾角公式
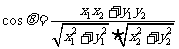 (a=
(a=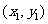 ,b=
,b=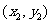 ).
).
l 平面兩點間的距離公式
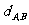 =
=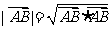
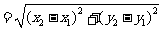 (A
(A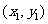 ,B
,B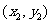 ).
).
l 向量的平行與垂直
設a=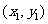 ,b=
,b=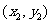 ,且b
,且b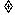 0,則
0,則
A||b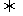 b=λa
b=λa 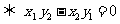 .
.
a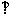 b(a
b(a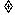 0)
0)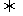 a·b=0
a·b=0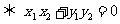 .
.
l 線段的定比分公式
設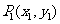 ,
,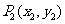 ,
,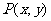 是線段
是線段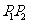 的分點,
的分點,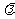 是實數,且
是實數,且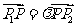 ,則
,則
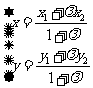
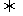
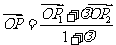
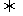
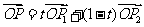 (
(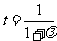 ).
).
l 三角形的重心坐標公式
△ABC三個頂點的坐標分別為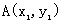 、
、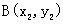 、
、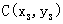 ,則△ABC的重心的坐標是
,則△ABC的重心的坐標是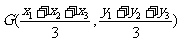 .
.
l 點的平移公式

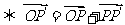 .
.
注:圖形F上的任意一點P(x,y)在平移后圖形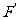 上的對應點為
上的對應點為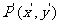 ,且
,且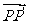 的坐標為
的坐標為 .
.
l “按向量平移”的幾個結論
(1)點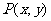 按向量a=
按向量a= 平移后得到點
平移后得到點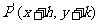 .
.
(2) 函數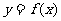 的圖象
的圖象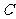 按向量a=
按向量a= 平移后得到圖象
平移后得到圖象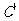 ,則
,則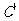 的函數解析式為
的函數解析式為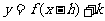 .
.
(3) 圖象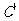 按向量a=
按向量a= 平移后得到圖象
平移后得到圖象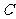 ,若
,若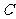 的解析式
的解析式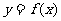 ,則
,則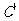 的函數解析式為
的函數解析式為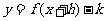 .
.
(4)曲線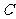 :
: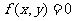 按向量a=
按向量a= 平移后得到圖象
平移后得到圖象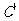 ,則
,則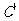 的方程為
的方程為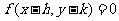 .
.
(5) 向量m=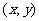 按向量a=
按向量a= 平移后得到的向量仍然為m=
平移后得到的向量仍然為m=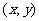 .
.
l 三角形五“心”向量形式的充要條件
設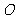 為
為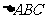 所在平面上一點,角
所在平面上一點,角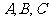 所對邊長分別為
所對邊長分別為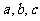 ,則
,則
(1)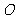 為
為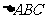 的外心
的外心 .
.
(2)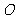 為
為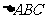 的重心
的重心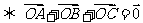 .
.
(3)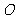 為
為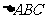 的垂心
的垂心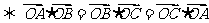 .
.
(4)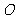 為
為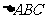 的內心
的內心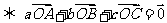 .
.
(5)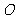 為
為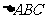 的
的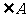 的旁心
的旁心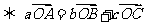 .
.
不等式
l 常用不等式:
(1)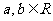

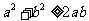 (當且僅當a=b時取“=”號).
(當且僅當a=b時取“=”號).
(2)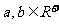

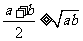 (當且僅當a=b時取“=”號).
(當且僅當a=b時取“=”號).
(3)
(4)柯西不等式
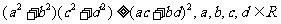
(5)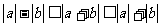 .
.
l 極值定理
已知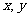 都是正數,則有
都是正數,則有
(1)若積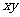 是定值
是定值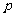 ,則當
,則當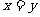 時和
時和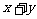 有最小值
有最小值 ;
;
(2)若和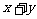 是定值
是定值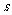 ,則當
,則當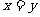 時積
時積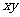 有最大值
有最大值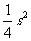 .
.
推廣 已知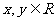 ,則有
,則有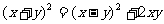
(1)若積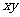 是定值,則當
是定值,則當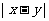 最大時,
最大時,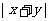 最大;
最大;
當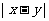 最小時,
最小時,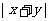 最小.
最小.
(2)若和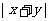 是定值,則當
是定值,則當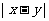 最大時,
最大時, 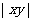 最小;
最小;
當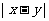 最小時,
最小時, 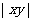 最大.
最大.
l
一元二次不等式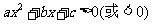
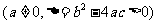 ,如果
,如果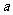 與
與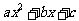 同號,則其解集在兩根之外;如果
同號,則其解集在兩根之外;如果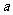 與
與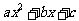 異號,則其解集在兩根之間.簡言之:同號兩根之外,異號兩根之間.
異號,則其解集在兩根之間.簡言之:同號兩根之外,異號兩根之間.
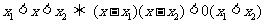 ;
;
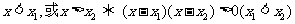 .
.
l 含有絕對值的不等式
當a> 0時,有
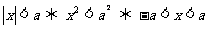 .
.
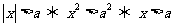 或
或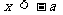 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com