
2、水的性質
物理性質:無色無味的液體、40C時密度最大,為1g/cm3
化學性質:通電分解
文字表達式:水(H2O) 氫氣(H2) + 氧氣(O2)
氫氣(H2) + 氧氣(O2)
化學方程式: 2H2O  2H2↑+O2↑
2H2↑+O2↑
1、水的組成:(考點一)
(1)電解水的實驗
A.裝置―――水電解器
B.電源種類---直流電
C.加入硫酸或氫氧化鈉的目的----增強水的導電性
D.化學反應:文字表達式::水(H2O) 氫氣(H2) + 氧氣(O2)
氫氣(H2) + 氧氣(O2)
|
 2H2↑+ O2↑
2H2↑+ O2↑
產生位置 負極 正極
體積比 2 : 1
質量比 1 : 8
E.檢驗:O2---出氣口置一根帶火星的木條----木條復燃
H2---出氣口置一根燃著的木條------氣體燃燒,發出淡藍色的火焰
(2)結論: ①水是由氫、氧元素組成的。
②化學變化中,分子可分而原子不可分。
20. 已知函數
已知函數
 上恒成立
上恒成立
(1)求 的值;
的值;
(2)若
(3)是否存在實數m,使函數 上有最小值-5?若
上有最小值-5?若
存在,請求出實數m的值;若不存在,請說明理由.
解:(1)


 恒成立
恒成立
即 恒成立
恒成立
顯然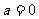 時,上式不能恒成立
時,上式不能恒成立
 是二次函數
是二次函數
由于對一切 于是由二次函數的性質可得
于是由二次函數的性質可得
 即
即
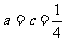 .
.
(2)


即
當 ,當
,當 .
.
(3)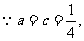


該函數圖象開口向上,且對稱軸為
假設存在實數m使函數 區間
區間 上有
上有
最小值-5.
①當 上是遞增的.
上是遞增的.

解得

 舍去
舍去
②當 上是遞減的,而在
上是遞減的,而在
區間 上是遞增的,
上是遞增的,

即
解得
③當 時,
時, 上遞減的
上遞減的

即
解得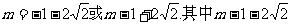 應舍去.
應舍去.
綜上可得,當 時,
時,
函數
19.數列{an}滿足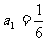 ,前n項和
,前n項和 ,
,
(1)寫出
(2)猜出 ,并用數學歸納法證明。
,并用數學歸納法證明。
解:(1)由 得:
得:
由 得:
得:
由 得:
得:
(2)猜想:
證明:①當n=1時,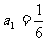 ,
, ,等式成立。
,等式成立。
②假設當n=k時等式成立,則 ,當n=k+1時,
,當n=k+1時,




 ,綜合①②,等式成立。
,綜合①②,等式成立。
17.一個均勻的正四面體的四個面上分別涂有1,2,3,4四個數字,現隨機投擲兩次,正四面體面朝下的數字分別為 ,記
,記 .
.
(1)分別求出 取得最大值和最小值時的概率;
取得最大值和最小值時的概率;
(2)求 的分布列及數學期望.
的分布列及數學期望.
解:(1)擲出點數 可能是:
可能是:
則 分別得:
分別得: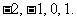 于是
于是 的所有取值分別為:
的所有取值分別為:
因此 的所有取值為:0,1,2,4,5,8.
的所有取值為:0,1,2,4,5,8.
當 且
且 時,
時, 可取得最大值
可取得最大值 ,
,
此時, ;
;
當 且
且 時,
時, 可取得最小值
可取得最小值 .
.
此時, .
.
(2)由(Ⅰ)知 的所有取值為:0,1,2,4,5,8.
的所有取值為:0,1,2,4,5,8.
 ;
;
當 =1時,
=1時, 的所有取值為(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值為(2,3)、(4,3)、(3,2)、(3,4).即 ;
;
當 =2時,
=2時, 的所有取值為(2,2)、(4,4)、(4,2)、(2,4).
的所有取值為(2,2)、(4,4)、(4,2)、(2,4).
即 ;
;
當 =4時,
=4時, 的所有取值為(1,3)、(3,1).即
的所有取值為(1,3)、(3,1).即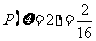 ;
;
當 =5時,
=5時, 的所有取值為(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值為(2,1)、(1,4)、(1,2)、(4,1).即 .
.
所以ξ的分布列為:
|
ξ |
0 |
1 |
2 |
4 |
5 |
8 |
|
P |
 |
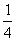 |
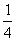 |
 |
 |
 |
18
已知函數 .
.
(Ⅰ)若函數 在
在 處取得極值,且曲線
處取得極值,且曲線 在點
在點
 ,
,
 處的切線與直線
處的切線與直線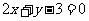 平行,求
平行,求 的值;
的值;
(Ⅱ)若 ,試討論函數
,試討論函數 的單調性.
的單調性.
解:(Ⅰ)函數 的定義域為
的定義域為 .
.
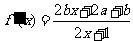
由題意 ,解得
,解得
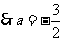 .
.
(Ⅱ)若 , 則
, 則 .
.
 .
.
(1)令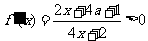 ,由函數定義域可知,
,由函數定義域可知, ,所以
,所以
①當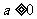 時,
時, ,
, ,函數
,函數 單調遞增;
單調遞增;
②當 時,
時, ,
, ,函數
,函數 單調遞增;
單調遞增;
(2)令 ,即
,即
①當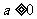 時,不等式
時,不等式 無解;
無解;
②當 時,
時, ,
, ,函數
,函數 單調遞減;
單調遞減;
綜上:當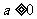 時,函數
時,函數 在區間
在區間 為增函數;
為增函數;
當 時,函數
時,函數 在區間
在區間 為增函數;
為增函數;
在區間 為減函數.
為減函數.
16. 在三棱錐
在三棱錐 中,
中, 和
和 是邊長為
是邊長為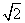 的等邊三角形,
的等邊三角形, ,
, 是
是 中點.
中點.
(Ⅰ)在棱 上求一點
上求一點 ,使得
,使得 ∥平面
∥平面 ;
;
(Ⅱ)求證:平面 ⊥平面
⊥平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
解
(Ⅰ)當 為棱
為棱 中點時,
中點時, ∥平面
∥平面 .
.
證明如下:
 分別為
分別為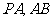 中點,
中點,

 ∥
∥
又 平面
平面 ,
, 平面
平面
 ∥平面
∥平面 .
.
(Ⅱ)連結 ,
,
 ,
, 為
為 中點,
中點, ,
,
 ⊥
⊥ ,
, .
.
同理,  ⊥
⊥ ,
,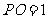 .
.
 又
又 ,
,
 ,
,
 .
.
 ⊥
⊥ .
.

 ⊥
⊥ ,
, ⊥
⊥ ,
,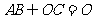 ,
,
 ⊥平面
⊥平面 .
.
 平面
平面
 平面
平面 ⊥平面
⊥平面 .
.
(Ⅲ)如圖,建立空間直角坐標系 .
.
則 ,
, ,
, ,
,
 ,
, .
.
由(Ⅱ)知 是平面
是平面
的一個法向量.
設平面 的法向量為
的法向量為 ,
,
則 .
.
令 ,則
,則 ,
,
 平面
平面 的一個法向量
的一個法向量 .
.
 .
.
 二面角
二面角 的平面角為銳角,
的平面角為銳角,
 所求二面角
所求二面角 的余弦值為
的余弦值為 .
.
15. 已知A,B,C為銳角 的三個內角,向量
的三個內角,向量 ,
,
 ,且
,且 .
.
(Ⅰ)求A的大小;(Ⅱ)求 取最大值時角B的大小.
取最大值時角B的大小.
解:(Ⅰ)
 ,
,



 .
.
 是銳角三角形,
是銳角三角形,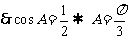 .
.
(Ⅱ) 是銳角三角形,且
是銳角三角形,且 ,
, 



當 取最大值時,
取最大值時, 即
即 .
.
14.若滿足 的實數
的實數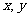 ,使不等式
,使不等式 恒成立,則實數
恒成立,則實數 的取值范圍是
的取值范圍是

13. 觀察以下不等式:


……
可以歸納出對于大于1的正整數n成立的一個不等式 ,則右端f(n)的表達式應該為
,則右端f(n)的表達式應該為 。
。
12. 直線 與曲線
與曲線 (
( 為參數,
為參數, )有兩個公共點
)有兩個公共點 ,且
,且 ,則實數
,則實數 的值為 2 ;在此條件下,以直角坐標系的原點為極點,
的值為 2 ;在此條件下,以直角坐標系的原點為極點, 軸正方向為極軸建立極坐標系,則曲線
軸正方向為極軸建立極坐標系,則曲線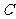 的極坐標方程為
的極坐標方程為 
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com