日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

6．物體A、B、C均靜止在同一水平面上，它們的質量分別為mA、mB、mC，與水平面的動摩擦因數分別為μA、μB、μC，用平行于水平面的拉力F分別拉物體A、B、C，所得加速度a與拉力F的關系如圖所示，A、B兩直線平行，則以下關系正確的是(　　 )

A．mA＜mB＜mC　　　　 B．mA＜mB=mC　　　　　　　

C．μA=μB=μC　　　　 D．μA＜μB=μC

5．如圖，柱體A的橫截面是圓心角為π/2的扇形面，其弧形表面光滑，而與地面接觸的下表面粗糙；在光滑豎直墻壁與柱體之間放置一質量為m的球體，系統處于平衡狀態。若使柱體向左移動少許，系統仍處于平衡狀態，則(　　　 )

　 A．球對墻的壓力減小

　 B．柱體與球之間的作用力增大　　

　 C．柱體所受的摩擦力減小

　 D．柱體對地面的壓力減小

4.舉世矚目的“神舟”七號航天飛船的成功發射和順利返回，顯示了我國航天事業取得的巨大成就．已知地球的質量為M，引力常量為G，設飛船繞地球做勻速圓周運動的軌道半徑為r，則飛船在圓軌道上運行的速率為(　 )　　　　　　　　　　　　　　　

2．下列光的波粒二象性的說法中，正確的是：(　 )

A．光有時是波，有時是粒子

B．光子與電子是同樣的粒子

C．大量光子的行為呈現波動性，個別光子的行為呈現粒子性

D．光的波長越長，其波動性越顯著，光的波長越短，其粒子性越顯著

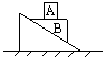　 3．如圖所示，A、B相對靜止，且一起沿斜面勻速下滑，斜面體靜止不動，則(　　 )

　 　　 A．A不受摩擦力

　 　　 B．A受到彈力大小等于A的重力大小

　 　　 C．B受到斜面對它的沿斜面向上的摩擦力的作用

　 　 　D．A、B之間必存在摩擦力　　

選對的得4分，選對不全給2分，有選錯或不選的得0分)

1．放在空氣中的玻璃磚，如圖所示，有一束光射到界面ah，下列說法正確的是：(　 )

A．在界面ab入射角大于臨界角的光將不會進入玻璃磚

B．無論入射角多大，光都能從界面ab進入玻璃磚

C．光傳播至界面cd后，有可能不從界面cd射出

D．無論入射角多大，光都能從界面cd射出

由于向量具有幾何形式和代數形式的“雙重身份”，使向量與解析幾何之間有著密切聯系，而新課程高考則突出了對向量與解析幾何結合考查，這就要求我們在平時的解析幾何教學與復習中，應抓住時機，有效地滲透向量有關知識，樹立應用向量的意識。應充分挖掘課本素材，在教學中從推導有關公式、定理，例題講解入手，讓學生去品位、去領悟，在公式、定理的探索、形成中逐漸體會向量的工具性，逐漸形成應用向量的意識，在教學中還應注重引導學生善于運用一些問題的結論，加以引申，使之成為解題方法，體會向量解題的優越性，在教學中還應注重引導學生善于運用向量方法解題，逐步樹立運用向量知識解題的意識.

例1、(2000年全國高考題)橢圓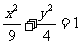的焦點為FF，點P為其上的動點，當∠FP F為鈍角時，點P橫坐標的取值范圍是___.

解：F₁(－,0)F₂(,0),設P(3cos,2sin)

為鈍角

∴ 　

　　 =9cos²－5+4sin²=5 cos²－1<0

　　 解得：　 ∴點P橫坐標的取值范圍是()

點評：解決與角有關的一類問題，總可以從數量積入手。本題中把條件中的角為鈍角轉化為向量的數量積為負值，通過坐標運算列出不等式，簡潔明了.

例2、已知定點A(-1,0)和B(1,0)，P是圓(x-3)²+(y-4)²=4上的一動點，求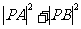的最大值和最小值.

分析：因為O為AB的中點，所以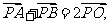故可利用向量把問題轉化為求向量的最值.

解：設已知圓的圓心為C，由已知可得：

又由中點公式得

所以

　　　　　　 =

　　　　　　 =

　　　　　　 =

又因為 點P在圓(x-3)²+(y-4)²=4上,　　　　　　　　　　　　　　　　

所以　 且　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

所以

即　 故

所以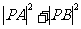的最大值為100，最小值為20.

點評：有些解幾問題雖然沒有直接用向量作為已知條件出現，但如果運用向量知識來解決，也會顯得自然、簡便，而且易入手.

例3、(2003年天津高考題)O是平面上一定點，A、B、C是平面上不共線的三個點，動點P滿足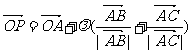，，則P的軌跡一定通過△ABC的(　 )

(A)外心　　　 (B)內心　　 (C)重心　　 (D)垂心

分析：因為同向的單位向量，由向量加法的平行四邊形則知是與∠ABC的角平分線(射線)同向的一個向量，又，知P點的軌跡是∠ABC的角平分線，從而點P的軌跡一定通過△ABC的內心.

反思：根據本題的結論，我們不難得到求一個角的平分線所在的直線方程的步驟；

(1)　　　　　　　　　　　 由頂點坐標(含線段端點)或直線方程求得角兩邊的方向向量；

(2)　　　　　　　　　　　 求出角平分線的方向向量

(3)　　　　　　　　　　　 由點斜式或點向式得出角平分線方程。{直線的點向式方程：過P()，其方向向量為，其方程為}

例4、(2003年天津)已知常數，向量，經過原點以為方向向量的直線與經過定點以為方向向量的直線相交于點，其中．試問：是否存在兩個定點，使得為定值，若存在，求出的坐標；若不存在，說明理由．

(本小題主要考查平面向量的概念和計算,求軌跡的方法，橢圓的方程和性質，利用方程判定曲線的性質，曲線與方程的關系等解析幾何的基本思想和綜合解題能力.)

解：根據題設條件，首先求出點P坐標滿足的方程，據此再判斷是否存在兩定點，使得點P到兩定點距離的和為定值.

∵，　 ∴=(λ，a)，=(1，－2λa).

因此，直線OP和AP的方程分別為　 　和 .

消去參數λ，得點的坐標滿足方程.

整理得　 ……①　　　 因為所以得：

(i)當時，方程①是圓方程，故不存在合乎題意的定點E和F；

　 (ii)當時，方程①表示橢圓，焦點和為合乎題意的兩個定點；

　 (iii)當時，方程①也表示橢圓，焦點和為合乎題意的兩個定點.

點評：本題以平面向量為載體，考查求軌跡的方法、利用方程判定曲線的性質、曲線與方程的關系等解析幾何的基本思想和綜合解題能力。去掉平面向量的背景，我們不難看到，本題即為下題：

在△OAP中，O(0，0)、A(0，a)為兩個定點，另兩邊OP與AP的斜率分別是，求P的軌跡.

而課本上有一道習題(數學第二冊(上)第96頁練習題4)：

三角形ABC的兩個頂點A、B的坐標分別是(-6，0)、(6，0)，邊AC、BC所在直線的斜率之積等于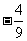，求頂點C的軌跡方程。通過本例可見高考題目與課本的密切關系.

例5．(2004年天津卷理22)橢圓的中心是原點O，它的短軸長為，相應于焦點F(c，0)()的準線與x軸相交于點A，|OF|=2|FA|，過點A的直線與橢圓相交于P、Q兩點.

　 (1)求橢圓的方程及離心率；

(2)若，求直線PQ的方程；

(3)設()，過點P且平行于準線的直線與橢圓相交于另一點M，證明.

分析：本小題主要考查橢圓的標準方程和幾何性質，直線方程，平面向量的計算，曲線和方程的關系等解析幾何的基本思想方法和綜合解題能力.

(1)解：由題意，可設橢圓的方程為.

　 由已知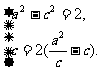得解得

所以橢圓的方程為，離心率.

(2)解：由(1)可得A(3，0).

設直線PQ的方程為.由方程組

　　　 得

依題意，得.

設，則，　 ① .　　 ②

由直線PQ的方程得.于是

.　　 ③

∵，∴.　　 ④

由①②③④得，從而.

所以直線PQ的方程為或

(2)證明：.由已知得方程組

　 注意，解得

因，故

.

而，所以.

平面向量是高中數學的新增內容，也是新高考的一個亮點。 向量知識、向量觀點在數學、物理等學科的很多分支有著廣泛的應用，它具有代數形式和幾何形式的“雙重身份”，能融數形與一體，能與中學數學教學內容的的許多主干知識綜合，形成知識交匯點。而在高中數學體系中，解析幾何占有著很重要的地位，有些問題用常規方法去解決往往運算比較繁雜，不妨運用向量作形與數的轉化，則會大大簡化過程.　

(十)社會生活

1、人們衣、食、住、行、用等方面的變化

衣：改革開放前，大多數人都穿“中山裝”和“解放裝”。改革開放后，物質生活的日益豐富為人們服飾的改變提供了基礎。現在，人們穿衣不再是單純為了保暖遮體，更多的是為了把自己打扮得更漂亮或展示獨特個性。

食：改革開放前，人們一般以粗糧為主，雞、鴨、肉難得一嘗。20世紀80年代以來，細糧成為人們的主要食物。如今，全國絕大多數人不僅能吃飽，而且許多人還講究要吃好，開始重視營養的全面與均衡了。

住：改革開放后，人們的住房條件有了很大改善。

行：改革開放以來，公路、鐵路、航空等交通設施發展非常迅速，四通八達的立體交通網已經形成，人們的出行越來越便捷。

用：改革開放前，條件好的家庭才有縫紉機、自行車、手表和收音機，當時叫“三轉一響”。改革開放后，電視機、洗衣機、空調等耐用消費品進入普通家庭。20世紀90年代以來，電話、電腦、手機這些昔日令人刮目相看的奢侈品，變得越來越普通，高檔住房、高級驕車已進入尋常百姓家。

2、就業制度的變化

在長期的計劃經濟體制下，在政府機關和國營企事業單位工作的人，職業和職位都非常穩定，人們形象地將其比喻為“鐵飯碗”。改革開放政策的實行，特別是社會主義市場經濟的建立，“鐵飯碗”逐漸被打破，各種形式的勞動就業和勞動合同制逐步推行。現在，勞動者自主擇業已占主導地位，以前人們“等、靠、要”的就業觀念正在轉變。

(九)科技、教育和文化

1、計算機網絡技術

計算機與互聯網技術是20世紀人類最偉大的發明之一。從20世紀80年代起，隨著計算機技術的廣泛運用，網絡技術異軍突起。網絡以其方便、快捷和多樣化的功能迅速深入到人們學習、工作和生活的方方面面，正在深刻地改變著整個世界。

我國于1986年開始網絡建設，1994年正式與國際互聯網連接。目前，我國正在加快發展信息技術和網絡技術，以信息化帶動工業化，力求實現社會經濟的跨越發展。

2、九年義務教育

1986年，六屆全國人大四次會議通過《中華人民共和國義務教育法》，規定我國要分階段實施九年制義務教育，從而為我國義務教育的談及提供了法律保障。

到2000年，全國基本普及了義務教育。

3.高等教育迅速發展

新中國成立以來，我國高等教育得到巨大發展。通過不斷深化改革，高校結構進一步改善，初步形成了多層次、多形式、學科門類基本齊全的高等教育體系。普通高等教育的辦學質量和效益也在不斷提高。我國對人才的培養也從過去以實用為目標的“專才”教育向“通才”教育方向發展。