
有的學生一看到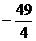 ,常受選擇答案(A)的誘惑,盲從附和。這正是思維缺乏反思性的體現(xiàn)。如果能以反思性的態(tài)度考察各個選擇答案的來源和它們之間的區(qū)別,就能從中選出正確答案。
,常受選擇答案(A)的誘惑,盲從附和。這正是思維缺乏反思性的體現(xiàn)。如果能以反思性的態(tài)度考察各個選擇答案的來源和它們之間的區(qū)別,就能從中選出正確答案。
利用一元二次方程根與系數(shù)的關(guān)系易得: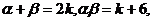

思路分析 本例只有一個答案正確,設了3個陷阱,很容易上當。
例7 設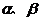 是方程
是方程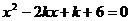 的兩個實根,則
的兩個實根,則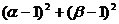 的最小值是( )
的最小值是( )
考察方程兩端相應的函數(shù)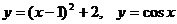 ,它們的圖象無交點。
,它們的圖象無交點。
所以此方程無解。
例6
解方程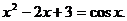
思考題:實數(shù)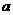 為何值時,圓
為何值時,圓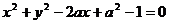 與拋物線
與拋物線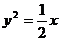 ,
,
(1) 有一個公共點;
(2) 有三個公共點;
(3) 有四個公共點;
(4) 沒有公共點。
養(yǎng)成驗算的習慣,可以有效地增強思維反思性。如:在解無理方程、無理不等式;對數(shù)方程、對數(shù)不等式時,由于變形后方程或不等式兩端代數(shù)式的定義域可能會發(fā)生變化,這樣就有可能產(chǎn)生增根或失根,因此必須進行檢驗,舍棄增根,找回失根。
(3) 獨立思考,敢于發(fā)表不同見解
受思維定勢或別人提示的影響,解題時盲目附和,不能提出自己的看法,這不利于增強思維的反思性。因此,在解決問題時,應積極地獨立思考,敢于對題目解法發(fā)表自己的見解,這樣才能增強思維的反思性,從而培養(yǎng)創(chuàng)造性思維。
例5 30支足球隊進行淘汰賽,決出一個冠軍,問需要安排多少場比賽?
解 因為每場要淘汰1個隊,30個隊要淘汰29個隊才能決出一個冠軍。因此應安排29場比賽。
思 路 分 析 傳統(tǒng)的思維方法是:30支隊比賽,每次出兩支隊,應有15+7+4+2+1=29場比賽。而上面這個解法沒有盲目附和,考慮到每場比賽淘汰1個隊,要淘汰29支隊,那么必有29場比賽。
因此,當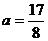 或
或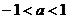 時,圓
時,圓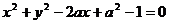 與拋物線
與拋物線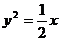 有兩個公共點。
有兩個公共點。
當方程①有一正根、一負根時,得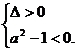 解之,得
解之,得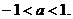
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com