
題目列表(包括答案和解析)
5.已知實數a、b滿足等式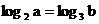 ,下列五個關系式:
,下列五個關系式:
① 0<a<b<1;② 0<b<a<1; ③ a=b;④ 1<a<b;⑤ l<b<a.
其中不可能成立的關系式有
A.1個 B.2個 C.3個 D.4個
4.若函數f (x)= e xsin x,則此函數圖象在點(4,f (4))處的切線的傾斜角為
A.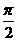 B.0 C.鈍角 D.銳角
B.0 C.鈍角 D.銳角
3.函數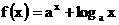 在區間[1,2]上的最大值與最小值之和為
在區間[1,2]上的最大值與最小值之和為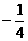 ,最大值與最小值之積為
,最大值與最小值之積為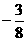 ,則a等于
,則a等于
A.2 B.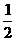 C.2或
C.2或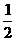 D.
D.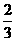
2.已知復數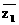 =a+i,z2=1+a 2 i,若
=a+i,z2=1+a 2 i,若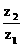 是實數,則實數a的值等于
是實數,則實數a的值等于
A.1 B.-1 C.-2 D.2
1.已知集合M={y| y=x+1},N={(x,y)|x
2 +y 2 =1},則M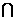 N中元素的個數是
N中元素的個數是
A.0 B.1 C.2 D.多個
22.(本題滿分18分)已知點A(0,1),
x、y Î R,m≥2,設 為直角坐標平面內x、y軸正方向上的單位向量,若向量
為直角坐標平面內x、y軸正方向上的單位向量,若向量 且
且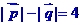 。
。
(1)求動點M (x, y )的軌跡方程,并指出方程所表示的曲線;
(2)設直線l : y = x - 3與點M的軌跡交于B、C兩點,問是否存在實數m,使得•= ?若存在,求出m的值;若不存在,試說明理由。
21.(本題滿分16分)已知數列 的前n項和為
的前n項和為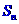 ,
, ,
,
(1)求數列 的通項公式;
的通項公式;
(2)設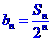 ,如果對一切正整數n都有
,如果對一切正整數n都有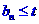 ,求t的最小值。
,求t的最小值。
20.(本題滿分14分)某銀行準備新設一種定期存款業務,經預測,存款量與存款利率成正比,比例系數為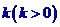 ,貸款的利率為6%,又銀行吸收的存款能全部放貸出去。
,貸款的利率為6%,又銀行吸收的存款能全部放貸出去。
(1)若存款的利率為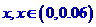 ,試分別寫出存款數量
,試分別寫出存款數量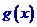 及銀行應支付給儲戶的
及銀行應支付給儲戶的
利息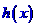 與存款利率
與存款利率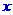 之間的關系式;
之間的關系式;
(2)存款利率定為多少時,銀行可獲得最大收益?
19.(本題滿分14分)已知正四棱柱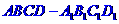 中,AB=2,
中,AB=2,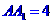 ,E為BC的中點,F為直線
,E為BC的中點,F為直線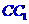
上動點。
(1)求異面直線 與
與 所成角的大小;
所成角的大小;
(2)(理)當F為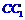 的中點時,求二面角
的中點時,求二面角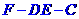 的大小
的大小
(文)當F為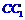 的中點時,求直線AF與平面
的中點時,求直線AF與平面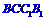 所成角的大小(用反三角函數表示);
所成角的大小(用反三角函數表示);
(3)證明:當點F在線段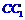 上移動時,三棱錐
上移動時,三棱錐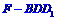 的體積是一個定值,并求出這個定值。
的體積是一個定值,并求出這個定值。

18.(本題滿分12分)已知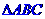 三個頂點分別是A(3,0)、B(0,3)、C
三個頂點分別是A(3,0)、B(0,3)、C ,
,
其中 。
。
(1)若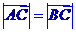 ,求角
,求角 的值;
的值;
(2)若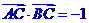 ,求
,求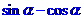 的值。
的值。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com