
2008年高考復習求解圓錐曲線問題易做易錯題選
圓錐曲線是中學數學教學的重點內容之一,也是歷屆高考命題的熱點,求解圓錐曲線問題時,學生應注意避免以下常見問題。
一、概念不清
例1 雙曲線 上的點P到點(5,0)的距離為8.5,求點P到點(
上的點P到點(5,0)的距離為8.5,求點P到點( )的距離。
)的距離。
錯解 設雙曲線的兩個焦點分別為 ,
, ,
,
由雙曲線定義知
所以 或
或
剖析 由題意知,雙曲線左支上的點到左焦點的最短距離為1,
所以 不合題意,事實上,在求解此類問題時,應靈活運用雙曲線定義,分析出點P的存在情況,然后再求解。如本題中,因左頂點到右焦點的距離為9>8.5,故點P只能在右支上,所求
不合題意,事實上,在求解此類問題時,應靈活運用雙曲線定義,分析出點P的存在情況,然后再求解。如本題中,因左頂點到右焦點的距離為9>8.5,故點P只能在右支上,所求
例2 已知圓 ,圓
,圓
 都內切于動圓,試求動圓圓心的軌跡方程。
都內切于動圓,試求動圓圓心的軌跡方程。
錯解:圓O2:
即為
所以圓O2的圓心為 ,半徑
,半徑 ,
,
而圓 的圓心為
的圓心為 ,半徑
,半徑 ,
,
設所求動圓圓心M的坐標為(x,y),半徑為r
則 且
且
所以
即
化簡得
即 為所求動圓圓心的軌跡方程。
為所求動圓圓心的軌跡方程。
剖析:上述解法將 =3看成
=3看成 ,誤認為動圓圓心的軌跡為雙曲線,這是雙曲線的概念不清所致。
,誤認為動圓圓心的軌跡為雙曲線,這是雙曲線的概念不清所致。
事實上,| 表示動點M到定點
表示動點M到定點 及
及 的距離差為一常數3。
的距離差為一常數3。
且 ,點M的軌跡為雙曲線右支,方程為
,點M的軌跡為雙曲線右支,方程為

二、忽視隱含條件
例3 點P與定點F(2,0)的距離和它到直線x=8的距離比是1:3,求動點P與定點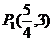 距離的最值。
距離的最值。
錯解:設動點P(x,y)到直線x=8的距離為d,則
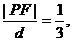
即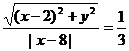
兩邊平方、整理得
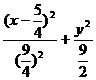 =1 (1)
=1 (1)
由此式可得:
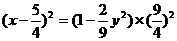
因為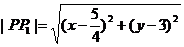
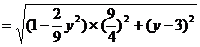
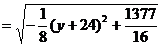
所以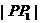
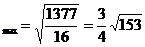
剖析 由上述解題過程知,動點P(x,y)在一橢圓上,由橢圓性質知,橢圓上點的橫縱坐標都是有限制的,上述錯解在于忽視了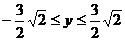 這一取值范圍,由以上解題過程知,
這一取值范圍,由以上解題過程知,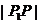 的最值可由二次函數在區間上的單調性給予解決
的最值可由二次函數在區間上的單調性給予解決
即:當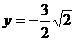 時,
時,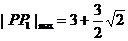
三、忽視元素之間的制約關系
例4 已知雙曲線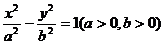 的離心率e=
的離心率e=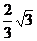 , 過點A(
, 過點A(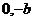 )和B(a,0)的直線與原點的距離為
)和B(a,0)的直線與原點的距離為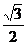 ,直線y=kx+m
,直線y=kx+m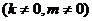 與該雙曲線交于不同兩點C、D,且C、D兩點都在以A為圓心的同一圓上,求m 的取值范圍。
與該雙曲線交于不同兩點C、D,且C、D兩點都在以A為圓心的同一圓上,求m 的取值范圍。
錯解 由已知,有
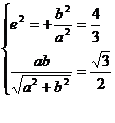
解之得: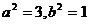
所以雙曲線方程為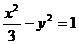
把直線 y=kx+m代入雙曲線方程,并整理得:
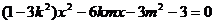
所以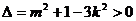 (1)
(1)
設CD中點為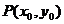 ,
,
則AP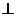 CD,且易知:
CD,且易知:
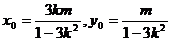
所以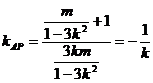
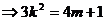 (2)
(2)
將(2)式代入(1)式得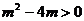
解得m>4或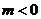
故所求m的范圍是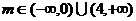
剖析 上述錯解,在于在減元過程中,忽視了元素之間的制約關系,將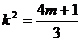 代入(1) 式時,m受k的制約。
代入(1) 式時,m受k的制約。
因為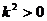
所以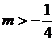
故所求m的范圍應為
m>4或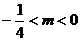
四、沒有分類意識
例5 橢圓中心是坐標原點,長軸在x軸上,離心率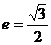 ,已知點P(
,已知點P(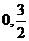 )到橢圓上的點最遠距離是
)到橢圓上的點最遠距離是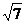 ,求這個橢圓的方程。
,求這個橢圓的方程。
錯解 設所求橢圓方程為
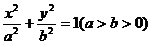
因為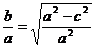
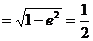
所以a=2b
于是橢圓方程為
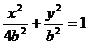
設橢圓上點M(x,y)到點P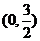 的距離為d,
的距離為d,
則: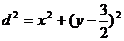
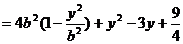
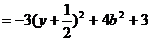
所以當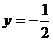 時,
時,
有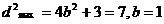
所以所求橢圓方程為
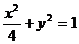
剖析 由橢圓方程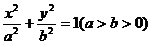
得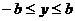
由(1)式知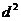 是y的二次函數,
是y的二次函數,
其對稱軸為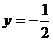
上述錯解在于沒有就對稱軸在區間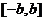 內或外進行分類,
內或外進行分類,
其正確應對f(y)=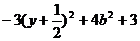 的最值情況進行討論:
的最值情況進行討論:
(1)當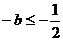 ,即
,即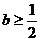 時
時
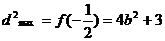 =7
=7
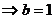 ,方程為
,方程為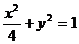
(2)當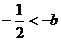 ,
,
即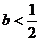 時,
時,
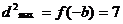
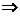
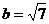
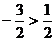 ,與
,與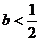 矛盾。
矛盾。
綜上所述,所求橢圓方程為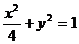
五、忽視判別式法。
例 6 已知雙曲線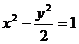 ,問過點A(1,1)能否作直線
,問過點A(1,1)能否作直線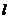 ,使
,使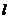 與雙曲線交于P、Q兩點,并且A為線段PQ的中點?若存在,求出直線
與雙曲線交于P、Q兩點,并且A為線段PQ的中點?若存在,求出直線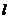 的方程,若不存在,說明理由。
的方程,若不存在,說明理由。
錯解 設符合題意的直線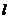 存在,并設
存在,并設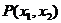 、
、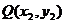
則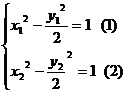
(1)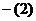 得
得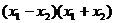
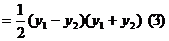
因為A(1,1)為線段PQ的中點,
所以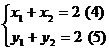
將(4)、(5)代入(3)得
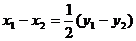
若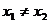 ,則直線
,則直線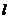 的斜率
的斜率
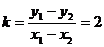
所以符合題設條件的直線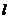 存在。
存在。
其方程為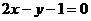
剖析 在(3)式成立的前提下,由(4)、(5)兩式可推出(6)式,但由(6)式不能推出(4)(5)兩式,故應對所求直線進行檢驗,上述錯解沒有做到這一點,故是錯誤的。
應在上述解題的基礎上,再由
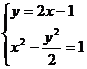
得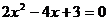
根據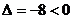 ,說明所求直線不存在。
,說明所求直線不存在。
六、忽視斜率不存在的情況。
例7 已知橢圓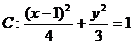 ,F為它的右焦點,直線
,F為它的右焦點,直線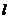 過原點交橢圓C于A、B兩點。求
過原點交橢圓C于A、B兩點。求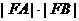 是否存在最大值或最小值?若不存在,說明理由。
是否存在最大值或最小值?若不存在,說明理由。
錯解 設A、B兩點坐標分別為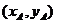 、
、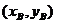
因為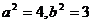
所以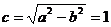
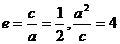
又橢圓中心為(1,0),右準線方程為x=5
所以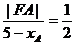
即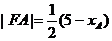
同理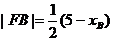
所以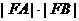
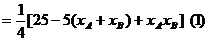
設直線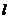 的方程為y=kx,代入橢圓方程得
的方程為y=kx,代入橢圓方程得
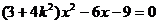
所以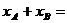
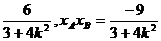
代入(1)式得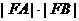
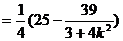
所以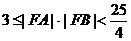
所以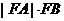 |有最小值3,無最大值。
|有最小值3,無最大值。
剖析 上述錯解過程忽視了過原點斜率不存在的直線,當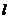 的斜率不存在時,有
的斜率不存在時,有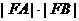
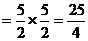
所以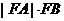 有最小值為 3,最大值為25/4
有最小值為 3,最大值為25/4
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com