
題目列表(包括答案和解析)
| |||||||||||
設有比例式![]() .
.
由比例性質可得:
![]() =
=![]() ,
,
![]() .
.
由此可得![]() =-1.
=-1.
試指出這個推理的錯誤所在.
在棱長為 的正方體
的正方體 中,
中, 是線段
是線段 的中點,
的中點, .
.
(1) 求證: ^
^ ;
;
(2) 求證: //平面
//平面 ;
;
(3) 求三棱錐 的表面積.
的表面積.

【解析】本試題考查了線線垂直和線面平行的判定定理和表面積公式的運用。第一問中,利用 ,得到結論,第二問中,先判定
,得到結論,第二問中,先判定 為平行四邊形,然后
為平行四邊形,然后 ,可知結論成立。
,可知結論成立。
第三問中, 是邊長為
是邊長為 的正三角形,其面積為
的正三角形,其面積為 ,
,
因為 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面積為
是直角三角形,其面積為 ,
,
同理 的面積為
的面積為 ,
,
 面積為
面積為 . 所以三棱錐
. 所以三棱錐 的表面積為
的表面積為 .
.
解: (1)證明:根據正方體的性質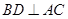 ,
,
因為 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)證明:連接 ,因為
,因為 ,
,
所以 為平行四邊形,因此
為平行四邊形,因此 ,
,
由于 是線段
是線段 的中點,所以
的中點,所以 , …………6分
, …………6分
因為
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是邊長為
是邊長為 的正三角形,其面積為
的正三角形,其面積為 ,
,
因為 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面積為
是直角三角形,其面積為 ,
,
同理 的面積為
的面積為 ,
……………………10分
,
……………………10分
 面積為
面積為 . 所以三棱錐
. 所以三棱錐 的表面積為
的表面積為

(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(文)對于數列 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為 ,公差為
,公差為 的無窮等差數列
的無窮等差數列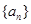 的子數列問題,為此,他取了其中第一項
的子數列問題,為此,他取了其中第一項 ,第三項
,第三項 和第五項
和第五項 .
.
(1) 若 成等比數列,求
成等比數列,求 的值;
的值;
(2) 在 ,
,  的無窮等差數列
的無窮等差數列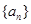 中,是否存在無窮子數列
中,是否存在無窮子數列 ,使得數列
,使得數列 為等比數列?若存在,請給出數列
為等比數列?若存在,請給出數列 的通項公式并證明;若不存在,說明理由;
的通項公式并證明;若不存在,說明理由;
(3) 他在研究過程中猜想了一個命題:“對于首項為正整數 ,公比為正整數
,公比為正整數 (
( )的無窮等比數 列
)的無窮等比數 列 ,總可以找到一個子數列
,總可以找到一個子數列 ,使得
,使得 構成等差數列”. 于是,他在數列
構成等差數列”. 于是,他在數列 中任取三項
中任取三項 ,由
,由 與
與 的大小關系去判斷該命題是否正確. 他將得到什么結論?
的大小關系去判斷該命題是否正確. 他將得到什么結論?
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(文)對于數列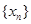 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為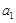 ,公差為
,公差為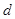 的無窮等差數列
的無窮等差數列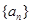 的子數列問題,為此,他取了其中第一項
的子數列問題,為此,他取了其中第一項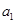 ,第三項
,第三項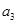 和第五項
和第五項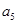 .
.
(1) 若 成等比數列,求
成等比數列,求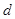 的值;
的值;
(2) 在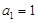 ,
, 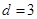 的無窮等差數列
的無窮等差數列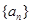 中,是否存在無窮子數列
中,是否存在無窮子數列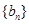 ,使得數列
,使得數列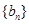 為等比數列?若存在,請給出數列
為等比數列?若存在,請給出數列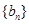 的通項公式并證明;若不存在,說明理由;
的通項公式并證明;若不存在,說明理由;
(3) 他在研究過程中猜想了一個命題:“對于首項為正整數 ,公比為正整數
,公比為正整數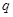 (
(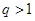 )的無窮等比數 列
)的無窮等比數 列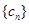 ,總可以找到一個子數列
,總可以找到一個子數列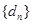 ,使得
,使得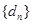 構成等差數列”. 于是,他在數列
構成等差數列”. 于是,他在數列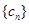 中任取三項
中任取三項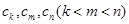 ,由
,由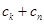 與
與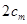 的大小關系去判斷該命題是否正確. 他將得到什么結論?
的大小關系去判斷該命題是否正確. 他將得到什么結論?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com