日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

3．一小型宇宙飛船在高空繞地球做勻速圓周運動如果飛船沿其速度相反的方向彈射出一個質量較大的物體，則下列說法中正確的是(　　 )．

　A．物體與飛船都可按原軌道運行

　B．物體與飛船都不可能按原軌道運行

　C．物體運行的軌道半徑無論怎樣變化，飛船運行的軌道半徑一定增加

　D．物體可能沿地球半徑方向豎直下落

2．兩名質量相等的滑冰人甲和乙都靜止在光滑的水平冰面上．現在其中一人向另一人拋出一個籃球，另一人接球后再拋回．如此反復進行幾次后，甲和乙最后的速率關系是　 (　　 )．

　A．若甲先拋球，則一定是V_甲>V_乙

　B．若乙最后接球，則一定是V_甲>V_乙

　C．只有甲先拋球，乙最后接球，才有V_甲>V_乙

D．無論怎樣拋球和接球，都是V_甲>V_乙　　

1．質量為m的人隨平板車以速度V在平直跑道上勻速前進，不考慮摩擦阻力，當此人相對于車豎直跳起至落回原起跳位置的過程中，平板車的速度　 (　　 )

　　 A．保持不變　　 B．變大　　 C．變小

　　 D．先變大后變小　 E．先變小后變大

5.如圖所示，人與冰車質量為M，球質量為m，開始均靜止于光滑冰面上，現人將球以對地速度V水平向右推出，球與擋板P碰撞后等速率彈回，人接住球后又將球以同樣的速度V向右推出……如此反復，已知M = 16 m，試問人推球幾次后將接不到球?

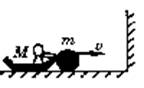
分析：(該題是多過程動量守恒問題，可以采用數學歸納的方法研究；當然也可整個過程采用動量定理研究)

解析： 　取水平向左為正方向，冰車、人、球為系統．由動量守恒定律，

對第一次推球過程有：　

對第二次整個接、推球過程有：

對第三次整個接、推球過程有：

　 對第n次整個接、推球過程同理分析得：　　

設推球n次后恰接不到球，則，故有　 代人已知條件

解得：n = 8.5，　　 即人推球9次后將接不到球．

三：動量守恒定律適應練習

丹陽六中　　 馬躍中

4．如圖所示，一塊足夠長的木板，放在光滑水平面上，在木板上自左向右并非放有序號是1，2，3，…，n的物體，所有物塊的質量均為m，與木板間的動摩擦因數都相同，開始時，木板靜止不動，第1，2，3，…n號物塊的初速度分別是v，2 v，3 v，…nv，方向都向右，木板的質量與所有物塊的總質量相等 ,最終所有物塊與木板以共同速度勻速運動。設物塊之間均無相互碰撞，木板足夠長。試求：

(1)所有物塊與木板一起勻速運動的速度v；

(2)第1號物塊與木板剛好相對靜止時的速度v；

(3)通過分析與計算說明第k號(k＜n＝物塊的最小速度v

分析：(多個物體組成的系統，應恰當選擇小系統利用動量守恒定律求解)

在木板上各個物塊相對木板運動，都給木板一個向右的磨擦力，因各個物塊質量相同，滑動磨擦力都一樣，木板在磨擦力的作用下向右加速。由于每個物塊的初始速度不同，因而相對木板靜止的物塊順序依次是1，2，…，n號，當第一號物塊由v到相對木板靜止時，其動量變化設為△p，則其他各個所有物塊在這段時間內的動量變化也都為△p(f相同，T相同)，因木板與所有物塊總動量守恒，故可用動量守恒關系求出第1號物塊相對木板靜止時的速度。

解析：(1)設所有物塊都相對木板靜止時的速度為 v，因木板與所有物塊系統水平方向不受外力，動量守恒，應有：

m v+m·2 v+m·3 v+…+m·n v=(M + nm)v　　　 1

　　　　　　 　M = nm，　 　　　　　　　　　　　　　　2

解得:　　　 　　v=(n+1)v，

　　 (2)設第1號物塊相對木板靜止時的速度為v，取木板與物塊1為系統一部分，第2 號物塊到第n號物塊為系統另一部分，則

　　　 木板和物塊1　　 △p =(M + m)v-m v，

　　　 2至n號物塊　　 △p=(n-1)m·(v- v)

由動量守恒定律： △p=△p，

解得　　　　　 　v= v，　　　　　　　　　　 3

(3)設第k號物塊相對木板靜止時的速度由v ，則第k號物塊速度由k v減為v的過程中，序數在第k號物塊后面的所有物塊動量都減小m(k v- v)，取木板與序號為1至K號以前的各物塊為一部分，則　

△p=(M+km)v-(m v+m·2 v+…+mk v)=(n+k)m v-(k+1)m v

序號在第k以后的所有物塊動量減少的總量為

　　 　△p=(n-k)m(k v- v)

由動量守恒得　 △p=△p， 即

(n+k)m v-(k+1)m v= (n-k)m(k v- v)，

解得　　　　 v=

3．質量為50㎏的人站在質量為150㎏(不包括人的質量)的船頭上，船和人以0.20m/s的速度向左在水面上勻速運動，若人用t =10s的時間勻加速從船頭走到船尾，船長L＝5m，則船在這段時間內的位移是多少？(船所受水的阻力不計)

分析：(該題利用動量守恒重點考查了人、船模型中速度關系、位移關系)

解析：設人走到船尾時，人的速度為，船的速度為　　　　　　　　　

　　 對系統分析：動量守恒

　　 對船分析：(勻加速運動) S =　

　　 對人分析：(勻加速運動) 　　

　　　　　　　　　　　　 得：S = 3.25 m.　　　　 　　　　

2．A、B兩滑塊在一水平長直氣墊導軌上相碰．用頻閃照相機在t₀＝0，t₁＝Δt，t₂＝2Δt，t₃＝3Δt各時刻閃光四次，攝得如圖所示照片，其中B像有重疊，m_B＝(3／2)m_A，由此可判斷　(　　　 )

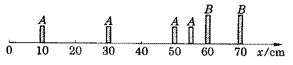A．碰前B靜止，碰撞發生在60cm處，t＝2.5Δt時刻 B．碰后B靜止，碰撞發生在60cm處，t＝0.5Δt時刻 C．碰前B靜止，碰撞發生在60cm處，t＝0.5Δt時刻 D．碰后B靜止，碰撞發生在60cm處，t＝2.5Δt時刻

解析：該題重點考查根據照片建立碰撞的物理圖景，答案為 B

1.放在光滑水平面上的A、B兩小車中間夾了一壓縮輕質彈簧，用兩手控制小車處于靜止狀態，下列說法正確的是　　 (　　 )

　　 A.兩手同時放開，兩車的總動量等于零

　　 B．先放開右手，后放開左手，兩車的總動量向右

　　 C．先放開右手，后放開左手，兩車的總動量向左

D．先放開右手，后放開左手，兩車的總動量為零

解析：該題考查動量守恒的條件，答案為 AB

4．動量恒定律的五個特性

①系統性：應用動量守恒定律時，應明確研究對象是一個至少由兩個相互作用的物體組成的系統，同時應確保整個系統的初、末狀態的質量相等

②矢量性：系統在相互作用前后，各物體動量的矢量和保持不變．當各速度在同一直線上時，應選定正方向，將矢量運算簡化為代數運算

③同時性：應是作用前同一時刻的速度，應是作用后同-時刻的速度

④相對性：列動量守恒的方程時，所有動量都必須相對同一慣性參考系，通常選取地球作參考系

⑤普適性：它不但適用于宏觀低速運動的物體，而且還適用于微觀高速運動的粒子．它與牛頓運動定律相比，適用范圍要廣泛得多，又因動量守恒定律不考慮物體間的作用細節，在解決問題上比牛頓運動定律更簡捷

二：典題分析

3．動量守恒定律的適用條件 ：

①系統不受外力或受到的外力之和為零(∑F_合=0)；

②系統所受的外力遠小于內力(F_外F_內)，則系統動量近似守恒；

③系統某一方向不受外力作用或所受外力之和為零，則系統在該方向上動量守恒(分方向動量守恒)