日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

5.一根內壁光滑的細圓管，形狀如下圖所示，放在豎直平面內，

一個小球自A口的正上方高h處自由落下，第一次小球恰能

抵達B點；第二次落入A口后，自B口射出，恰能再進入

A口，則兩次小球下落的高度之比h₁：h₂=　　 ______

4.　 長為L質量分布均勻的繩子，對稱地懸掛在輕小的定滑輪上，

如圖所示.輕輕地推動一下，讓繩子滑下，那么當繩子離

開滑輪的瞬間，繩子的速度為　　　　　　　　　　　　　 　.

3．一物體從某一高度自由落下，落在直立于地面的輕彈簧上，如圖所示．在A點時，物體開始接觸彈簧；到B點時，物體速度為零，然后被彈回．下列說法中正確的是 [bcd　　 ]

　A．物體從A下降到B的過程中，動能不斷變小

　B．物體從B上升到A的過程中，動能先增大后減小

　C．物體由A下降到B的過程中，彈簧的彈性勢能不斷增大

　D．物體由B上升到A的過程中，彈簧所減少的彈性勢能等于物體所增加的動能與增加的重力勢能之和

2．質量為m的物體，在距地面h高處以g /3的加速度由靜止豎直下落到地面，

下列說法中正確的是：　　　 (　　　　　　　　　 )

A.　 物體的重力勢能減少 1/3 mgh

B.　 物體的機械能減少 2/3 mgh

C.　 物體的動能增加 1/3 mgh

D.　 重力做功 mgh

1．在光滑水平面上有兩個相同的彈性小球A、B，質量都為m. 現B球靜止，A球向B球運動，發生正碰。已知碰撞過程中總機械能守恒，兩球壓縮最緊時的彈性勢能為E_p，則碰前A球的速度等于　 (　　　　　 )

3.　

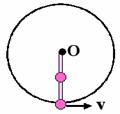例1、如圖示，長為l 的輕質硬棒的底端和中點各固定一個質量為m的小球，為使輕質硬棒能繞轉軸O轉到最高點，則底端小球在如圖示位置應具有的最小速度v= 　　　　　　　　　　。

解：系統的機械能守恒，ΔE_P +ΔE_K=0

因為小球轉到最高點的最小速度可以為0 ，所以，

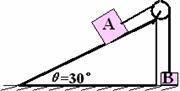
例 2. 如圖所示，一固定的楔形木塊，其斜面的傾角θ=30°，另一邊與地面垂直，頂上有一定滑輪。一柔軟的細線跨過定滑輪，兩端分別與物塊A和B連結，A的質量為4m，B的質量為m，開始時將B按在地面上不動，然后放開手，讓A沿斜面下滑而B上升。物塊A與斜面間無摩擦。設當A沿斜面下滑S 距離后，細線突然斷了。求物塊B上升離地的最大高度H.

解：對系統由機械能守恒定律

4mgSsinθ – mgS = 1/2× 5 mv²

∴　 v²=2gS/5

細線斷后，B做豎直上拋運動，由機械能守恒定律

mgH= mgS+1/2× mv²

∴　 H = 1.2 S　 　

例 3. 如圖所示，半徑為R、圓心為O的大圓環固定在豎直平面內，兩個輕質小圓環套在大圓環上．一根輕質長繩穿過兩個小圓環，它的兩端都系上質量為m的重物，忽略小圓環的大小。

(1)將兩個小圓環固定在大圓環豎直對稱軸的兩側θ=30°的位置上(如圖)．在

兩個小圓環間繩子的中點C處，掛上一個質量M= m的重物，使兩個小圓

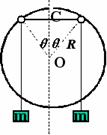環間的繩子水平，然后無初速釋放重物M．設繩子

與大、小圓環間的摩擦均可忽略，求重物M下降的最大距離．

(2)若不掛重物M．小圓環可以在大圓環上自由移動，且繩子與大、小圓環間及大、小圓環之間的摩擦均可以忽略，問兩個小圓環分別在哪些位置時，系統可處于平衡狀態?

解：(1)重物向下先做加速運動，后做減速運動，當重物速度

　為零時，下降的距離最大．設下降的最大距離為h ，

由機械能守恒定律得

解得　

(另解h=0舍去)

(2)系統處于平衡狀態時，兩小環的可能位置為

a．　 兩小環同時位于大圓環的底端．

b．兩小環同時位于大圓環的頂端．

c．兩小環一個位于大圓環的頂端，另一個位于大圓環的底端．

d．除上述三種情況外，根據對稱性可知，系統如能平衡，則兩小圓環的位置一定關于大圓環豎直對稱軸對稱．設平衡時，兩小圓環在大圓環豎直對稱軸兩側α角的位置上(如圖所示)．

對于重物，受繩子拉力與重力作用， 有T=mg

對于小圓環，受到三個力的作用，水平繩的拉力T、 豎直繩子的拉力T、大圓環的支持力N.

兩繩子的拉力沿大圓環切向的分力大小相等，方向相反

得α=α′, 而α+α′=90°，所以α=45 °

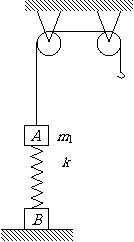例 4. 如圖質量為m₁的物體A經一輕質彈簧與下方地面上的質量為m₂的物體B相連，彈簧的勁度系數為k，A、B都處于靜止狀態。一條不可伸長的輕繩繞過輕滑輪，一端連物體A，另一端連一輕掛鉤。開始時各段繩都牌伸直狀態，A上方的一段沿豎直方向。現在掛鉤上掛一質量為m₃的物體C上升。若將C換成另一個質量為(m₁+m₃)物體D，仍從上述初始位置由靜止狀態釋放，則這次B則離地時D的速度的大小是多少？已知重力加速度為g。

解:開始時，B靜止平衡，設彈簧的壓縮量為x_1,

掛C后，當B剛要離地時，設彈簧伸長量為x₂，有

此時，A和C速度均為零。從掛C到此時，根據機械能守恒定律彈簧彈性勢能的改變量為

將C換成D后，有

聯立以上各式可以解得

針對訓練

2.　 對機械能守恒定律的理解：

(1)系統在初狀態的總機械能等于末狀態的總機械能.

即　 　E₁ = E₂ 或　　 1/2mv₁² + mgh₁= 1/2mv₂² + mgh₂

(2)物體(或系統)減少的勢能等于物體(或系統)增加的動能，反之亦然。

即　　　　　 -ΔE_P = ΔE_K

(3)若系統內只有A、B兩個物體，則A減少的機械能E_A等于B增加的機械能ΔE _B即　　　　　 -ΔE_A = ΔE_B

_{二、例題導航：}

1.　 在只有重力和彈簧的彈力做功的情況下，物體的動能和勢能發生相互轉化，但機械能的總量保持不變.

10．選木箱、人和小車組成的系統為研究對象，取向右為正方向.設第n次推出木箱后人與小車的速度為v_n,第n次接住后速度為v_n′,則由動量守恒定律可知：

第一次推出后有：0=Mv₁-mv,則v₁=mv/M

第一次接住后有：Mv₁+mv=(M+m)v₁′

第二次推出后有：(M+m)v₁′=Mv₂-mv,則v₂=3mv/M

第二次接住后有：Mv₂+mv=(M+m)v₂′……

第n-1次接住：Mv_n-1+mv=(M+m)v_n-1

第n次推出：(M+m)v_n-1′=Mv_n-mv　　　　 　　即v_n=(2n-1)mv/M

設最多能推N次，推出后有v_n≥v　 v_n-1≤v　 即≥v,且＜v

所以 ≤ N ＜ + 1　　　 將M/m=4代入，可得： 2.5≤N＜3.5 　

因N取整數，故N=3

9．(1)射出第一顆子彈時，設船的速度為V₁，由動量守恒定律得，

(2)每射出一顆子彈的過程，系統的動量均守恒，而每一顆子彈進入靶中后，船的速度將為零，故每一顆子彈射出時，船后退的速度是相同的，

即

　　 (3)每發射一顆子彈的過程實際上經歷了三個階段：第一階段是擊發到子彈射出槍瞠為止；第二個階段是子彈在空中飛行的階段；第三個階段是子彈從擊中靶子到靜止為止．三個階段都遵從動量守恒定律，第一、第三階段歷時很短，故這兩個階段船的移動可忽略．因此每發射一顆子彈的過程，只在第二階段船向后移動．每發射完一顆子彈后船向移動的距離