
1.某國際機構在美國首都華盛頓(西五區)主持視頻會議,請中國的王教授在北京給遠在非洲(西一區至東三區)的同行介紹經驗。下列時段中,對三方最合適的是
A.華盛頓時間14:00-16:00 B.北京時間14:00-16:00
C.華盛頓時間2l:00-23:00 D.北京時間21:00-23:00
9. (1)因為BE∥AC,AB∥CD,
所以四邊形ABEC是平行四邊形,
所以CE=AB=4,
所以△AED的面積為 ×4×(4×2)=16;
×4×(4×2)=16;
(2)四邊形APCD的面積與正方形ABCD的面積相等,
因為BE∥AC,所以△APC的面積與△ABC的面積相等,
所以△APC的面積+△ACD的面積=△ABC的面積+△ACD的面積=正方形ABCD的面積;
8. 解:(1)在△ABC中由已知得:BC=2,AC=AB×cos30°= ,
,
∴AB1=AC+C B1=AC+CB= .……………………………………2分
.……………………………………2分
(2)四邊形A2B1DE為平行四邊形.理由如下:
∵∠EDG=60°,∠A2B1C1=∠A1B1C=∠ABC=60°,∴A2B1∥DE
又A2B1=A1B1=AB=4,DE=4,∴A2B1=DE,故結論成立.………………4分
(3)由題意可知:
S△ABC= ,
,
①
當 或
或 時,y=0
時,y=0
此時重疊部分的面積不會等于△ABC的面積的一半……………5分
②當 時,直角邊B2C2與等腰梯形的下底邊DG重疊的長度為DC2=C1C2-DC1=(x-2)㎝,則y=
時,直角邊B2C2與等腰梯形的下底邊DG重疊的長度為DC2=C1C2-DC1=(x-2)㎝,則y= ,
,
當y=  S△ABC=
S△ABC=  時,即
時,即
 ,
,
解得 (舍)或
(舍)或 .
.
∴當 時,重疊部分的面積等于△ABC的面積的一半.
時,重疊部分的面積等于△ABC的面積的一半.
③當 時,△A3B2C2完全與等腰梯形重疊,即
時,△A3B2C2完全與等腰梯形重疊,即 ……………7分
……………7分
④當 時,B2G=B2C2-GC2=2-(
時,B2G=B2C2-GC2=2-(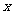 -8)=10-
-8)=10-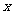
則y= ,
,
當y=  S△ABC=
S△ABC=  時,即
時,即
 ,
,
解得 ,或
,或 (舍去).
(舍去).
∴當 時,重疊部分的面積等于△ABC的面積的一半.………9分
時,重疊部分的面積等于△ABC的面積的一半.………9分
由以上討論知,當 或
或 時, 重疊部分的面積等于△ABC的面積的一半.………10分
時, 重疊部分的面積等于△ABC的面積的一半.………10分
7. 解:(1)過C點作CG⊥AB于G,
在Rt△AGC中,∵sin60°= ,
,
∴ ··································· 1分
··································· 1分
∵AB=2,∴S梯形CDBF=S△ABC= ······················ 3分
······················ 3分
(2)菱形···································· 4分
∵CD∥BF, FC∥BD,∴四邊形CDBF是平行四邊形·················· 5分
∵DF∥AC,∠ACD=90°,∴CB⊥DF························· 6分
∴四邊形CDBF是菱形······························ 7分
(判斷四邊形CDBF是平行四邊形,并證明正確,記2分)
(3)解法一:過D點作DH⊥AE于H,則S△ADE= ······· 8分
······· 8分
又S△ADE= ,
, ················· 9分
················· 9分
∴在Rt△DHE’中,sinα= ·················· 10分
·················· 10分
解法二:∵△ADH∽△ABE··························· 8分
∴
即:
∴ ·································· 9分
·································· 9分
∴sinα= ····················· 10分
····················· 10分

6. 解:(1) ;···················· 2分
;···················· 2分
 ;····················· 4分
;····················· 4分
 ;················· 6分
;················· 6分
 (2)
(2) ;························· 8分
;························· 8分
(3) (
( 為正整數). 10分
為正整數). 10分
5. 解 (1) 由題意,得∠A=90°,c=b,a= b,
b,
∴a2–b2=( b)2–b2=b2=bc.············· 3分
b)2–b2=b2=bc.············· 3分
(2) 小明的猜想是正確的.·············· 4分
理由如下:如圖3,延長BA至點D,使AD=AC=b,連結CD,
 ·························· 5分
·························· 5分
則ΔACD為等腰三角形.
∴∠BAC=2∠ACD,又∠BAC=2∠B,∴∠B=∠ACD=∠D,∴ΔCBD為等腰三角形,即CD=CB=a, 6分
又∠D=∠D,∴ΔACD∽ΔCBD,············ 7分
∴ .即
.即 .∴a2=b2+bc.∴a2–b2= bc·· 8分
.∴a2=b2+bc.∴a2–b2= bc·· 8分
(3) a=12,b=8,c=10.·············· 10分
3. (1)  ,
,  ,
0,
,
0, 
 , 0,
, 0,  , 0;
, 0;
2, 1, 3, 2;
 ,
,  .
.
(2)已知: 和
和 是方程
是方程 的兩個根,
的兩個根,
那么, ,
,  .
.
2. 解:(1)由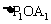 是等腰直角三角形,得
是等腰直角三角形,得 ,則有
,則有 ,故
,故
 (負舍),點
(負舍),點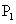 (2,2)。
(2,2)。
(2)由題意知

又 ,則
,則
則 ,故
,故 ,同理,依次得
,同理,依次得
1. 解:通過觀察凸四邊形和五邊形對角線的條數,可得到凸八邊形的對角線條數應該是20條.思考過程:凸n邊形每個頂點不能和它自己以及它的兩個鄰點作對角線,所以可做的對角線條數是(n-3), 凸n邊形有n個頂點,所以可做n(n-3)條,由于對角線AB和BA是同一條,所以凸n邊形共有
解:通過觀察凸四邊形和五邊形對角線的條數,可得到凸八邊形的對角線條數應該是20條.思考過程:凸n邊形每個頂點不能和它自己以及它的兩個鄰點作對角線,所以可做的對角線條數是(n-3), 凸n邊形有n個頂點,所以可做n(n-3)條,由于對角線AB和BA是同一條,所以凸n邊形共有 條對角線.當n=8時,有
條對角線.當n=8時,有 條對角線.
條對角線.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com