日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

8．(2009·江西省重點中學一次聯考)已知定義域為R的函數y＝f(x)在(－∞，a)(a>0)上是增函數，且函數y＝f(x+a)是偶函數，當x₁<a，x₂>a，|x₁－a|<|x₂－a|時有(　)

A．f(2a－x₁)>f(2a－x₂)

B．f(2a－x₁)＝f(2a－x₂)

C．f(2a－x₁)<f(2a－x₂)

D．f(2a－x₁)與f(2a－x₂)的大小關系不確定

答案：A

解析：由y＝f(x+a)是偶函數得f(－x+a)＝f(x+a)，即f(x)＝f(2a－x)，于是f(x₁)＝f(2a－x₁)，f(x₂)＝f(2a－x₂)．由x₁<a，x₂>a，|x₁－a|<|x₂－a|得2a－x₂<a，a－x₁<x₂－a,2a－x₂<x₁<a.又函數f(x)在(－∞，a)上是增函數，因此有f(2a－x₂)<f(x₁)，f(2a－x₂)<f(2a－x₁)，選A.

7．(2009·西安地區八校聯考)設函數f(x)、g(x)的定義域分別為F、G，且F?G.若對任意的x∈F，都有g(x)＝f(x)，則稱g(x)為f(x)在G上的一個“延拓函數”．已知函數f(x)＝2^x(x≤0)，若g(x)為f(x)在R上的一個延拓函數，且g(x)是偶函數，則函數g(x)的解析式是(　)

A．2^|x|　 　　　　　　　　　　　　　　　　　　　　　　　 B．log₂|x|

C．()^|x|　 　　　　　　　　　　　　　　　　　　　　　　 D．log|x|

答案：C

解析：由題意得，當x≤0時，g(x)＝f(x)＝2^x＝2^－|x|.又g(x)是偶函數，因此有g(－x)＝g(x)恒成立．當x>0時，－x<0，g(x)＝g(－x)＝2^－x＝()^|x|.綜上所述，g(x)＝()^|x|，選C.

6．(2009·成都市一測)已知a>0，且a≠1，若函數f(x)＝log_a(x+)在(－∞，+∞)上既是奇函數，又是增函數，則函數g(x)＝log_a|x－k|的圖象是(　)

5．(2008·湖北省八校聯考)定義在R上的函數f(x)的圖象關于點(－，0)成中心對稱，對任意的實數x都有f(x)＝－f(x+)，且f(－1)＝1，f(0)＝－2，則f(1)+f(2)+f(3)+…+f(2008)的值為(　)

A．－2　 　　　　　　　　　　　　　　　　　　　　　　 B．－1

C．0　 　　　　　　　　　　　　　　　　　　　　　　　　 D．1

答案：D

解析：函數f(x)的圖象關于點(－，0)成中心對稱，得f(x)+f(－－x)＝0，又f(x)＝－f(x+)，于是f(x)是偶函數，且f(x)＝－f(x+)＝f(x+3)，即3是函數f(x)的周期，f(－1)＝1＝f(2)＝f(1)＝f(4)，f(0)＝－2＝f(3)，

f(1)+[f(2)+f(3)+f(4)]+…+[f(2006)+f(2007)+f(2008) ＝f(1)＝1.故選D.

4．(2009·徐水模擬)已知f(x)是以2為周期的奇函數，當0<x<1時，f(x)＝lgx，設a＝f()，b＝f()，c＝f()，則(　)

A．a<b<c　 　　　　　　　　　　　　　　　　　　　　 B．b<a<c

C．c<b<a　 　　　　　　　　　　　　　　　　　　　　 D．c<a<b

答案：D

解析：a＝f()＝－f(－)＝－f(－+2)＝－f()

b＝f()＝－f(－)＝－f()，c＝f()＝f()

由當0<x<1時，f(x)＝lgx得c<a<b.

3．(2008·北京市西城區抽樣測試)設函數f(x)＝.若f(x)是奇函數，則g(2)的值是(　)

A．－　 　　　　　　　　　　　　　　　　　　　　　　 B．－4

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．4

答案：A

解析：∵f(x)是奇函數，∴f(－x)＝－f(x)；∵f(x)＝，當x>0時，－x<0，f(－x)＝－f(x)＝2^－x，∴g(x)＝－2^－x(x>0)，g(2)＝－，故選A.

2．(2009·北京市西城區4月)設a為常數，f(x)＝x²－4x+3，若函數f(x+a)為偶函數，則a等于(　)

A．－2　　　　　　　　　　　 B．2

C．－1 　　　　　　　　　　　　　　　　　　　　　　　 D．1

答案：B

解析：依題意，由f(x+a)＝(x+a)²－4(x+a)+3＝x²+(2a－4)x+(a²－4a+3)是偶函數，因此2a－4＝0，a＝2，選B.

1．f(x)，g(x)是定義在R上的函數，h(x)＝f(x)+g(x)，則“f(x)，g(x)均為偶函數”是“h(x)為偶函數”的(　)

A．充要條件

B．充分而不必要條件

C．必要而不充分條件

D．既不充分也不必要條件

答案：B

解析：充分性易證：∵h(－x)＝f(－x)+g(－x)＝f(x)+g(x)＝h(x)對x∈R恒成立，∴h(x)是偶函數．

但h(x)為偶函數，推不出f(x)，g(x)均為偶函數，反例如f(x)＝x，g(x)＝－x，h(x)＝0.雖然h(x)＝0為偶函數，但f(x)、g(x)卻都不是偶函數．故選B.

4．⑴3NaClO₃+3H₂SO₄＝2ClO₂↑+HClO₄+H₂O+3NaHSO₄或3NaClO₃+2H₂SO₄＝2ClO₂↑+NaClO₄+H₂O+2NaHSO₄ ；⑵二氧化硫作為還原劑把ClO₂還原為NaClO₂、2ClO₂+SO₂+4OH^－＝2ClO₂^－+SO₄^2－+2H₂O；(3)H₂SO₄

21世紀教育網

2.0－x) mol•L^－1　　 x mol•L^－1　　　 K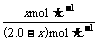＝＝＝0.042　 x＝0.081(0.084也給分)；處理次數＝＝2.5(2.38也給分)。至少處理3次；⑷節能，環保