
21.解:(I)由題意知, …………………..2分
…………………..2分
由橢圓定義知,動點 滿足的曲線
滿足的曲線 方程是:
方程是: …………………4分
…………………4分
(II)由方程組

 ……………………………………………….7分
……………………………………………….7分
 的面積
的面積 ………10分
………10分

 不存在直線
不存在直線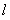 滿足題意……………….12分
滿足題意……………….12分
20.(滿分12分)某自來水廠的蓄水池存有400噸水,水廠每小時可向蓄水池中注水60噸,同時蓄水池又向居民小區不間斷供水, 小時內供水總量為
小時內供水總量為 噸,(
噸,( )
)
(1)從供水開始到第幾小時時,蓄水池中的存水量最少?最少水量是多少噸?
(2)若蓄水池中水量少于80噸時,就會出現供水緊張現象,請問:在一天的24小時內,有幾小時出現供水緊張現象。
解:(1)設 小時后蓄水池中的水量為
小時后蓄水池中的水量為 噸,
噸,
則 ; --------------------3分
; --------------------3分
令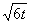 =
= ;則
;則 ,即
,即
 ;--5分
;--5分
∴當 ,即
,即 時,
時, ,
,
即從供水開始到第6小時時,蓄水池水量最少,只有40噸。--------7分
(2)依題意 ,得
,得 ----------10分
----------10分
解得, ,即
,即 ,
, ;
;
即由 ,所以每天約有8小時供水緊張。--------------12分
,所以每天約有8小時供水緊張。--------------12分
19.(滿分12分)已知函數 的定義域為
的定義域為 ,
(1)求M ,(2)當
,
(1)求M ,(2)當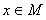 時,求
時,求
 的最小值.
解 (1)
的最小值.
解 (1)
 (…………4分)
(…………4分)
(2) =
=
又 ,
, ,
, (…………………6分)
(…………………6分)
①若 ,即
,即 時,
時, =
=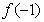 =
= ,(…………8分)
,(…………8分)
②若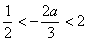 ,即
,即
 時,
時,
所以當 即
即 時,
時, =
= (………………11分)
(………………11分)
 ……………………………………………….12分
……………………………………………….12分
18.解:(1) 當 時,
時, ,
,
則

∴ 當
當 時,
時,  , ………………………….3分
, ………………………….3分
則
 ,
,
∴
綜上所述, 對于 , 都有
, 都有 ,
,
∴ 函數 是偶函數。………………………………………………….6分
是偶函數。………………………………………………….6分
(2)當 時,
時, 
設 , 則
, 則 .…………………8分
.…………………8分
當 時,
時,  ;
;
當 時,
時,  ,
,
∴ 函數 在
在 上是減函數, 函數
上是減函數, 函數 在
在 上是增函數。….12分
上是增函數。….12分
17.由x2-2x+1-m2≤0,得1-m≤x≤1+m(m>0),…………………….3分
由 得-2≤
得-2≤ 即-2≤x≤10.………………..6分
即-2≤x≤10.………………..6分
則非p:x<-2或x>10. ………………………………………….7分
非q:x>1+m或x<1-m(m>0).………………………………….8分
若非p是非q的必要不充分條件,則:
∴m≥9 ………………………………………………………………….12分
17.(滿分12分)已知p: ,q:
,q: ,若非p是非q的必要而不充分條件,求實數m的取值范圍.
,若非p是非q的必要而不充分條件,求實數m的取值范圍.
14. 9+10+11 ,4+5+6+7+8 ,6+7+8+9 (選對其中兩個即可)
13.
 14.
14.  13.
13.
1-3 B B D C D D
A D B D A B
22.(滿分14分)已知函數
(1)若 處取得極值,求實數a的值;
處取得極值,求實數a的值;
(2)在(1)的條件下,若關于x的方程 上恰有兩個不同的實數根,求實數m的取值范圍;
上恰有兩個不同的實數根,求實數m的取值范圍;
(3)若存在 ,使得不等式
,使得不等式 成立,求實數a的取值范圍。
成立,求實數a的取值范圍。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com