日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

2.向量的運算

運算類型	幾何方法	坐標方法	運算性質
向量的 加法	1.平行四邊形法則 2.三角形法則
向量的 減法	三角形法則		,
數 乘 向 量	1.是一個向量,滿足: 2.>0時, 同向; <0時, 異向; =0時, .
向 量 的 數 量 積	是一個數 1.時， . 2.

1.向量的概念

(1)向量的基本要素：大小和方向.(2)向量的表示：幾何表示法 ；字母表示：a；

坐標表示法 a＝xi+yj＝(x，y).

(3)向量的長度：即向量的大小，記作｜a｜.

(4)特殊的向量：零向量a＝O｜a｜＝O.

單位向量：a_O為單位向量｜a_O｜＝1.

(5)相等的向量：大小相等，方向相同(x₁，y₁)＝(x₂，y₂)

(6) 相反向量：a=-bb=-aa+b=0

(7)平行向量(共線向量)：方向相同或相反的向量，稱為平行向量.記作a∥b.平行向量也稱為共線向量.

10．中，內角..的對邊分別為..，已知..成等比數列，且

(1)求的值；

(2)若，求的值

解:(1)由得：

由及正弦定理得：

于是：

(2)由得：，因，所以：，即：

由余弦定理得：

于是：

故：a+c

[探索題](2005上海)對定義域是.的函數.，

規定：函數

(1)若函數，，寫出函數的解析式；

(2)求問題(1)中函數的值域；

(3)若，其中是常數，且，請設計一個定義域為R的函數，及一個的值，使得，并予以證明

　[解] (1)

　 (2) 當x≠1時, h(x)= =x－1++2,

　　　 若x>1時, 則h(x)≥4,其中等號當x=2時成立

若x<1時, 則h(x)≤ 0,其中等號當x=0時成立

∴函數h(x)的值域是(－∞,0]∪{1}∪[4,+∞)

(3)令 f(x)=sin2x+cos2x,α=

則g(x)=f(x+α)= sin2(x+)+cos2(x+)=cos2x－sin2x,

于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x－sin2x)=cos4x.

另解令f(x)=1+sin2x, α=,

g(x)=f(x+α)= 1+sin2(x+π)=1－sin2x,

于是h(x)= f(x)·f(x+α)= (1+sin2x)( 1－sin2x)=cos4x.

9． P是以F₁、F₂為焦點的橢圓上一點，且∠PF₁F₂=α，∠PF₂F₁=2α，求證：橢圓的離心率為e=2cosα－1.

剖析：依據橢圓的定義2a=|PF₁|+|PF₂|，2c=|F₁F₂|，

∴e=.

在△PF₁F₂中解此三角即可得證.

證明：在△PF₁F₂中，由正弦定理知

==.

由比例的性質得=

e===

=

==2cosα－1.

評述：恰當地利用比例的性質有事半功倍之效.

8．為進行科學實驗，觀測小球A、B在兩條相交成角的直線型軌道上運動的情況，如圖所示，運動開始前，A和B分別距O點3m和1m，后來它們同時以每分鐘4m的速度各沿軌道按箭頭的方向運動。問：

　 (I)運動開始前，A、B的距離是多少米？(結果保留三位有效數字)。

　 (Ⅱ)幾分鐘后，兩個小球的距離最小？

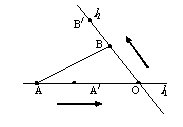
解：小球開始運動前的距離為：

　 (2)設t分鐘后，小球A、B分別運動到A’、B’處，則

當時，

當時，

故

當，

故分鐘后兩個小球的距離最小。

7．(1)已知，求角的集合;

(2)已知cosx=-0.4,x∈[0,2π],求角x的集合.

解：先找出一個周期上的角,再加上周期.

(1)　　 在上,;　

在上,,

所求角x的集合為：

(常寫成)

(2)　　 當;

當

綜上得

5.; 6. y=.令=m，m∈(，1)，

則y=－2m²+3m－1.∈(0，］.

[解答題]

6. 已知x∈(0，),則函數y=的值域是_________.

◆練習簡答：1-4. BBCA；4.由.sinA=sin(B+C)=－cosBcosC，得tanB+tanC=－1.

又tan(B+C)==－，tanA=.… A=.

5.函數y=sinx－cosx的圖象可由y=sinx+cosx的圖象向右平移_______個單位得到.

4.(2005啟東市調研)在斜△ABC中，sinA=－cosBcosC且tanBtanC=1－，則∠A的值為 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　 )

A.　　　　　　　 B.　　　　　　　 C.　　　　　　 D.

[填空題]