日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

2.讀圖，回答下列問題。

(1)寫出圖中字母、數字代表的內容：A.　　　　　　　　 B.　　　　　　 　　C.　　　　　　　　 a.　　　　　 b.　　　　　　　 c.　　　　　　　 。

(2)陸地自然資源包括　　　　　　　 資源、　　　　　　　　 資源、　　　　　　　　　 資源和生物資源。其中　　　　　　　　 資源屬于非可再生資源。

(3)假若A地有豐富的森林資源，那么該地發展的社會第一級生產是　　　　　 ，在此基礎上還可發展　　　

　　　　 業和　　　　　　 　業。

(4)從圖中可知，人類主要是通過　　　　　 與環境發生關系的，在協調系統平衡中起　　　　　　 作用。

(5)假若A地煤、鐵資源豐富，那么工業化時期以后，該地區的人口　　　　　 ，原因是　　　　　　　　　　　　 。

(6)陸地自然資源是人類文明和社會進步的物質基礎，是人類進行生產活動的　　　　　　　　　 。

答案　 (1)自然資源　 陸地環境　 廢棄物　 消費流通　 生產、生活排放　 改造控制

(2)礦產　 土地　 水　 礦產　 ?(3)林?業　 木材加工　 造紙　

(4)對自然資源的開發利用　 核心　 (5)增長過快　 工業化時期以后，煤鐵資源成為發展生產的重要資源

(6)對象

命題視角　 自然資源特點及其分布、應用

[例](2007·北京文綜)資源短缺和市場有限往往制約著一個國家的發展。歷史上，許多國家為了獲取資源、爭奪市場采用了非和平的手段。我國政府明確指出，中國堅持走和平發展道路。完成下列問題。

以一種陸地資源為例，說明其特點和分布規律。

答案　 (1)舉例：礦產、土地、水、生物資源(舉出任意一種即可)

(2)特點和分布：①數量有限，利用潛力無限；②各種資源相互影響；③分布不均；④土地、水、生物資源分布一般具有地帶性，礦產資源的分布受地質條件制約。

子　 變式演練

(2008·上海地理)當前，水資源緊缺已成為許多國家與地區經濟發展的嚴重障礙，人們正在采取多種措施擺脫這一困境。

(1)通常所說的水資源，是指目前人類可以大量利用的　　　　　　　　　　　　　　　　　　　 (　　 )

A.冰川水、河水、湖泊水　　　　　　　　　　　 B.河水、淡水湖泊水、淺層地下水

C.冰川水、大氣水、土壤水　　　　　　　　　　 D.大氣水、淡水湖泊水、沼澤水

(2)根據自然條件與用水需求等因素判斷，下列四組國家中，水資源都非常緊缺的一組是　　　　　　 (　　 )

A.埃及、新加坡　　　　　 B.巴西、阿根廷　 C.英國、以色列　　　 D.美國、墨西哥

(3)跨流域調水是解決地區水資源不足的措施之一。下列國家中，根據本國自然環境特點進行大規模“東水西調”的是 　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.俄羅斯　　　　　　 B.加拿大　　　　　　　　 C.中國　　　　　　　 D.澳大利亞

答案　 (1)B　 (2)A　 (3)D

住宅與氣象、氣候的關系是十分密切的。在我國的春聯中常常可以看到“向陽門第春常在”這句話，意思是說一個住宅如果能經常得到陽光的照射，家人就會心情舒暢、精神愉快、健康長壽。住宅區房屋的建筑要充分利用當地氣候的有利因素，避開不利因素，尋求適應于當地氣候特點的建筑形式，利用建筑自身的調節能力創造怡人的小氣候。據此回答1-3題。

1.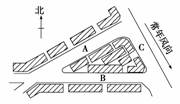讀“某小區規劃設計圖”，回答下列問題。

(1)從光照條件分析，A、B、C三條街道規劃合理的是　　　　　　　　　　　 ，理由是　　　　　　　　　 。

(2)居住區最好布局在小區　　　　　　　　　　　 方向。

(3)該小區的工業區應布局在小區的　　　　　　　　　 地區，理由是　　　　　　　　 　　　。

(4)若小區地處季風地區，夏季風與圖中風向相反，則工業區應布局在小區的　　　　　　　　 地區。

答案　 (1)AC　 只有當街道與子午線成30°-60°夾角時，街道兩側所有建筑物才有較好的日照條件

(2)西北　 (3)東南　 使工業區位于常年風向的下風向，可減少工廠排放污染物對小區的影響

(4)東北或西南

考點二　 陸地資源

子　 強化專練

解法二　 設S_x＝Ax²+Bx(x∈N)

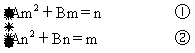
①－②，得A(m²－n²)+B(m－n)＝n－m

∵m≠n　 ∴ A(m+n)+B=－1

故A(m+n)²+B(m+n)＝－(m+n)

即S_m+n＝－(m+n)

說明　 a₁，d是等差數列的基本元素，通常是先求出基本元素，再

解的“整體化”思想，在解有關數列題目中值得借鑒．解法二中，由于是等差數列，由例22，故可設S_x=Ax²+Bx．(x∈N)

[例14]　 在項數為2n的等差數列中，各奇數項之和為75，各偶數項之和為90，末項與首項之差為27，則n之值是多少？

解　 ∵S_偶項－S_奇項=nd

∴nd=90－75=15

又由a_2n－a₁＝27，即(2n－1)d=27

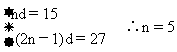
[例15]　 在等差數列{a_n}中，已知a₁＝25，S₉＝S₁₇，問數列前多少項和最大，并求出最大值．

解法一　 建立S_n關于n的函數，運用函數思想，求最大值．

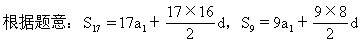
∵a₁=25，S₁₇＝S₉　 解得d＝－2

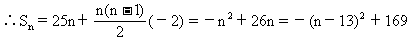
∴當n=13時，S_n最大，最大值S₁₃＝169

解法二　 因為a₁=25＞0，d＝－2＜0，所以數列{a_n}是遞減等

∵a₁＝25，S₉＝S₁₇

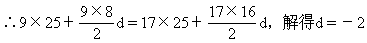
∴a_n=25+(n－1)(－2)=－2n+27

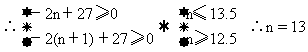
即前13項和最大，由等差數列的前n項和公式可求得S₁₃=169．

解法三　 利用S₉=S₁₇尋找相鄰項的關系．

由題意S₉=S₁₇得a₁₀+a₁₁+a₁₂+…+a₁₇=0

而a₁₀+a₁₇=a₁₁+a₁₆=a₁₂+a₁₅=a₁₃+a₁₄

∴a₁₃+a₁₄＝0，a₁₃=－a₁₄　 ∴a₁₃≥0，a₁₄≤0

∴S₁₃=169最大．

解法四　 根據等差數列前n項和的函數圖像，確定取最大值時的n．

∵{a_n}是等差數列

∴可設S_n＝An²+Bn

二次函數y=Ax²+Bx的圖像過原點，如圖3．2－1所示

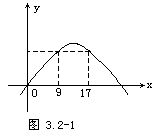
∵S₉＝S₁₇，

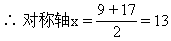
∴取n=13時，S₁₃＝169最大

3．要掌握對數列各項的同加、同減、同乘以某一個不等于零的數的變形方法，將其轉化為常見的一些數列．

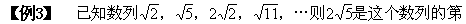
幾項．

[例4]　 已知下面各數列{a_n}的前n項和S_n的公式，求數列的通項公式．

(1)S_n＝2n²－3n　　 (2)S_n＝n²+1

(3)S_n＝2ⁿ+3 　(4)S_n＝(－1)ⁿ⁺¹·n

解　 (1)當n=1時，a₁=S₁＝－1；

當n≥2時，a_n＝S_n－S_n-1=(2n²－3n)－[2(n－1)²－3(n－1)]＝4n－5，由于a₁也適合此等式，因此a_n=4n－5．

(2)當n＝1時，a₁＝S₁=1+1＝2；

當n≥2時，a_n＝S_n－S_n-1=n²+1－[(n－1)²+1]＝2n－1，由于a₁不適合于此等式，

(3)當n＝1時，a₁=S₁＝2+3=5；

當n≥2時，a_n=S_n－S_n-1＝2ⁿ+3－(2^n-1+3)＝2^n-1，由于a₁不適合于此等式，

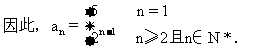
(4)當n＝1時，a₁＝S₁=(－1)²·1=1；

當n≥2時，a_n＝S_n－S_n-1=(－1)ⁿ⁺¹·n－(－1)ⁿ·(n－1)=(－1)ⁿ⁺¹(2n－1)，由于a₁也適可于此等式，因此a_n＝(－1)ⁿ⁺¹(2n－1)，n∈N*．

說明　 已知S_n求a_n時，要先分n＝1和n≥2兩種情況分別進行計算，然后驗證能否統一．

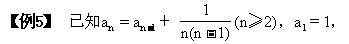
(1)寫出數列的前5項；

(2)求a_n．

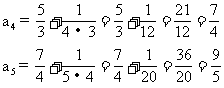
(2)由第(1)小題中前5項不難求出．

[例6]　 數列{a_n}中，a₁＝1，對所有的n≥2，都有a₁·a₂·a₃·…·a_n＝n²．

(1)求a₃+a₅；

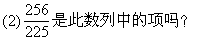
解　 由已知：a₁·a₂·a₃·…·a_n＝n²得

說明　 (1)“知和求差”、“知積求商”是數列中常用的基本方法．

(2)運用方程思想求n，若n∈N*，則n是此數列中的項，反之，則不是此數列中的項．

[例7]　 已知數a_n=(a²－1)(n³－2n)(a=≠±1)是遞增數列，試確定a的取值范圍．

解法一　 ∵數列{a_n}是遞增數列，∴a_n+1＞a_n

a_n+1－a_n＝(a²－1)[(n+1)³－2(n+1)]－(a²－1)(n³－2n)

＝(a²－1)[(n+1)³－2(n+1)－n³+2n]

＝(a²－1)(3n²+3n－1)

∵(a²－1)(3n²+3n－1)＞0

又∵n∈N*，∴3n²+3n－1=3n(n+1)－1＞0

∴a²－1＞0，解得a＜－1或a＞1．

解法二　 ∵{a_n}是遞增數列，∴a₁＜a₂即：

(a²－1)(1－2)＜(a²－1)(8－4)

化簡得　 a²－1＞0

∴a＜－1或a＞1

說明　 本題從函數的觀點出發，利用遞增數列這一已知條件，將求取值范圍的問題轉化為解不等式的問題

2．對于常見的一些數列的通項公式(如：自然數列，a_n=n；自然數的平方數列，a_n＝n²；奇數數列，a_n＝2n－1；偶數數列，a_n=2n；

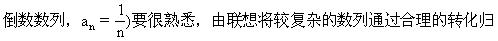
納出數列的通項公式．

1．用歸納法寫出數列的一個通項公式，體現了由特殊到一般的思維規律．對于項的結構比較復雜的數列，可將其分成幾個部分分別考慮，然后將它們按運算規律結合起來．

2．

由eU₀=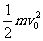得電子入射速度

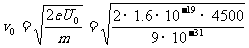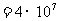m/sm/s　　 　

(1)加直流電壓時，板間場強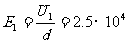V/m　　　 　

電子做直線運動時，由條件eE₁= ev₀B，

得應加磁場的磁感應強度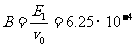T，　　 　

方向垂直紙面向里。　　　　 　

(2)加交流電壓時，A、B兩極間場強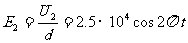(V/m)

電子飛出板間時偏距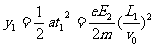　　 　

電子飛出板間時豎直速度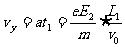　 　

從飛離板到達圓筒時偏距

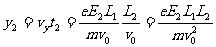
在紙上記錄落點的總偏距　

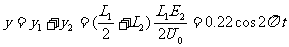(m) 　

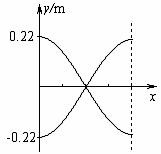
可見，在記錄紙上的點以振幅0.20m，周期T=1s作簡諧運動，

因圓筒每秒鐘轉2周，故在1s內，紙上圖形如圖所示。

1.

解： (1)因為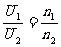，所以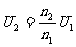=2 500 V(3分)..

(2) P₂=P₁=50 kW(1分)..

輸電線中電流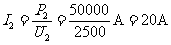(1分)..

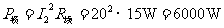則(2分)..

(3)用戶得到功率P₄ =P₂ 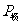－ =44 000 W(2分)..

所以降壓變壓器副線圈電流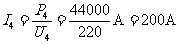(1分)..

故(2分)..

2.　 (1) A、B　 (2) 260

1.　 A