
19.(本小題滿分16分)已知數列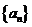 的首項為
的首項為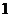 ,
,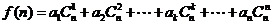
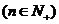 .
.
(1)若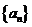 為常數列,求
為常數列,求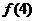 的值;
的值;
(2)若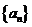 為公比為
為公比為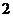 的等比數列,求
的等比數列,求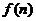 的解析式;
的解析式;
(3)數列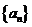 能否成等差數列,使得
能否成等差數列,使得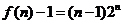 對一切
對一切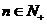 都成立.若能,求出數列
都成立.若能,求出數列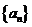 的通項公式;若不能,試說明理由.
的通項公式;若不能,試說明理由.
18.(本小題滿分16分)已知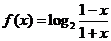
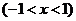 .
.
(1)若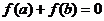 ,求證:
,求證: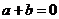 ;
;
(2)設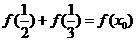 ,求
,求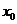 的值;
的值;
(3)設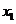 、
、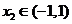 ,是否存在
,是否存在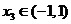 ,使得
,使得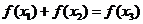 ,若存在,求出
,若存在,求出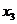 ,并證明你的結論;若不存在,請說明理由.
,并證明你的結論;若不存在,請說明理由.
17.(本小題滿分14分)某游樂場舉辦“迎國慶”有獎射擊活動,規定參與者每人射擊三次,三次全中,獎勵價值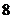 元的小禮品;中兩次且連中,獎勵價值
元的小禮品;中兩次且連中,獎勵價值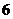 元的小禮品;中兩次但不連中,獎勵價值
元的小禮品;中兩次但不連中,獎勵價值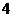 元的小禮品;只中一次,獎勵價值
元的小禮品;只中一次,獎勵價值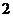 元的小禮品;不中的則沒有獎品.設某人射擊一次中靶的概率為
元的小禮品;不中的則沒有獎品.設某人射擊一次中靶的概率為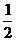 ,用
,用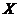 表示獲得獎品的金額數.
表示獲得獎品的金額數.
(1)求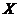 的概率分布表;
的概率分布表;
(2)求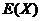 .
.
16.(本題滿分14分)在直角坐標系中以原點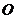 為極點,
為極點,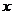 軸的正半軸為極軸建立極坐標系,且在兩種坐標系中取相同的長度單位.已知圓
軸的正半軸為極軸建立極坐標系,且在兩種坐標系中取相同的長度單位.已知圓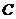 的圓心的極坐標
的圓心的極坐標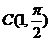 ,半徑
,半徑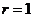 ,直線
,直線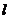 的參數方程為
的參數方程為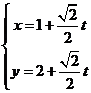 (
(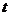 為參數).
為參數).
(1)求圓的極坐標方程,并將極坐標方程化成直角坐標方程;
(2)將直線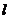 的參數方程化為普通方程,并判斷直線
的參數方程化為普通方程,并判斷直線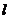 與圓
與圓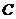 的位置關系.
的位置關系.
15.(本題滿分14分)已知復數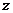 滿足
滿足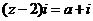
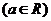 .
.
(1)求復數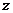 ;(2)
;(2)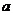 為何值時,復數
為何值時,復數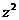 對應點在第一象限.
對應點在第一象限.
14.一袋中裝有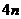 只紅球和
只紅球和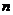 只黑球(所有球的形狀、大小都相同),每一次從袋中摸出兩只球,且每次摸球后均放回袋中. 現規定:摸出的兩只球顏色不同則為中獎.設三次摸球恰有一次中獎的概率為
只黑球(所有球的形狀、大小都相同),每一次從袋中摸出兩只球,且每次摸球后均放回袋中. 現規定:摸出的兩只球顏色不同則為中獎.設三次摸球恰有一次中獎的概率為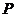 ,則當
,則當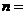 ▲ 時,使得
▲ 時,使得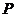 最大.
最大.
13.已知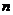 是給定的正整數,整數
是給定的正整數,整數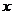 、
、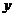 滿足不等式
滿足不等式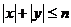 ,則整數對
,則整數對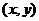 的個數為
的個數為
▲ .

12.連續3次拋擲一枚質地均勻的硬幣,在至少有一次出現正面向上的條件下,恰有一次出現反面向上的概率為 ▲ .
11.在平面直角坐標系中,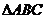 的頂點
的頂點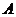 、
、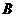 分別是離心率為
分別是離心率為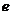 的圓錐曲線
的圓錐曲線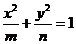 的焦點,頂點
的焦點,頂點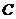 在該曲線上.一同學已正確地推得:當
在該曲線上.一同學已正確地推得:當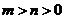 時,有
時,有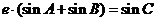 .類似地,當
.類似地,當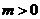 、
、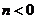 時,有
時,有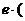 ▲
▲ 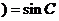 .
. 
10.定義在實數集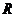 上的函數
上的函數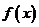 滿足
滿足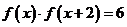 ,若
,若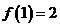 ,則
,則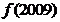 的值為 ▲ .
的值為 ▲ .
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com