
5.空間兩條異面直線的畫法
4.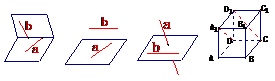 等角定理的推論:若兩條相交直線和另兩條相交直線分別平行,那么這兩條直線所成的銳角(或直角)相等.
等角定理的推論:若兩條相交直線和另兩條相交直線分別平行,那么這兩條直線所成的銳角(或直角)相等.
3.等角定理:若一個角的兩邊和另一個角的兩邊分別平行并且方向相同,則這兩個角相等
1  空間兩直線的位置關系(1)相交--有且只有一個公共點;(2)平行--在同一平面內,沒有公共點;(3)異面--不在任何一個平面內,沒有公共點;
空間兩直線的位置關系(1)相交--有且只有一個公共點;(2)平行--在同一平面內,沒有公共點;(3)異面--不在任何一個平面內,沒有公共點;
2.公理4 :平行于同一條直線的兩條直線互相平行 推理模式:
推理模式: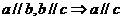 .
.
10. 已知:空間四邊形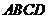 ,
,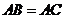 ,
,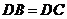 ,求證:
,求證: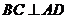
證明:取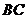 中點
中點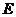 ,連結
,連結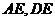 ,∵
,∵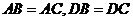 ,∴
,∴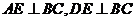 ,
,
∴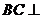 平面
平面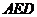 ,又∵
,又∵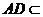 平面
平面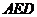 ,∴
,∴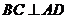 .
.
9.如圖,已知ABCD是矩形,SA⊥平面ABCD,E是SC上一點.
求證:BE不可能垂直于平面SCD.
證明:用到反證法,假設BE⊥平面SCD,
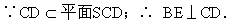 ∵ AB∥CD;∴AB⊥BE.
∵ AB∥CD;∴AB⊥BE.


∴ AB⊥SB,這與Rt△SAB中∠SBA為銳角矛盾.
∴ BE不可能垂直于平面SCD 
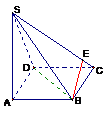
8.點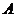 為
為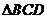 所在平面外的一點,點
所在平面外的一點,點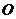 為點
為點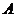 在平面
在平面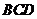 內的射影,
內的射影,
若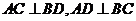 ,求證:
,求證: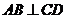 .
.
證明:連結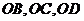 ,∵
,∵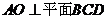 ,且
,且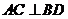
∴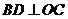 (三垂線定理逆定理)
(三垂線定理逆定理)
同理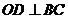 ,∴
,∴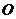 為
為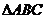 的垂心,∴
的垂心,∴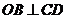 ,
,
 又∵
又∵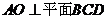 ,∴
,∴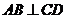 (三垂線定理)
(三垂線定理)
3.能否作一條直線同時垂直于兩條相交直線?能否作一條直線同時垂直于兩個相交平面?為什么?
答案:(能,而且有無數條) (不能)
4 拿一張矩形的紙對折后略為展開,豎立在桌面上,說明折痕為什么和桌面垂直
拿一張矩形的紙對折后略為展開,豎立在桌面上,說明折痕為什么和桌面垂直
答案:因為折痕垂直于桌面內的兩條相交直線.
5 一條直線垂直于一個平面內的兩條平行直線,這條直線垂直于這個平面嗎?為什么?
一條直線垂直于一個平面內的兩條平行直線,這條直線垂直于這個平面嗎?為什么?
答案:不一定.因為這條直線可能與這個平面斜交或在其內.
6 過一點和一條直線垂直的平面是否只有一個?為什么?
過一點和一條直線垂直的平面是否只有一個?為什么?
答案:是.假若有兩個平面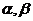 過點A都于
過點A都于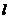 垂直,過這條公共垂線
垂直,過這條公共垂線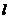 作一個不經過兩平面
作一個不經過兩平面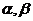 的交線的平面
的交線的平面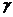 ,
,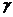 與
與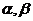 分別相交于直線
分別相交于直線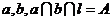 且
且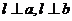 ,
,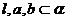 ,從而有
,從而有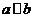 ,此與
,此與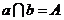 矛盾.
矛盾.
7 如果三條直線共點,且兩兩垂直,問其中一條直線是否垂直于另兩條直線所確定的平面
如果三條直線共點,且兩兩垂直,問其中一條直線是否垂直于另兩條直線所確定的平面
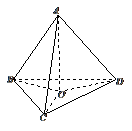 答案:是
答案:是
2.(1)過直線外一點作直線的垂線有 條;垂面有 個;平行線有 條;平行平面有 個.(2)過平面外一點作該平面的垂線有 條;垂面有 個;平行線有 條;平行平面有 個.
答案:(1)無數,一,一,無數;(2)一,無數,無數,一
1.(1)“直線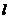 垂直于平面a內的無數條直線”是“
垂直于平面a內的無數條直線”是“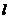 ⊥a”的 ( )
⊥a”的 ( )
(A)充分條件(B)必要條件(C)充要條件(D)既不充分也不必要條件
(2)如果一條直線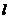 與平面a的一條垂線垂直,那么直線
與平面a的一條垂線垂直,那么直線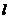 與平面a的位置關系是( )
與平面a的位置關系是( )
(A)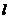 Ìa (B)
Ìa (B)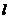 ⊥a (C)
⊥a (C)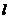 ∥a (D)
∥a (D)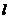 Ìa或
Ìa或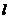 ∥a 答案:(1)B (2)D
∥a 答案:(1)B (2)D
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com