
題目列表(包括答案和解析)
1.(安徽卷)如果實數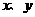 滿足條件
滿足條件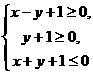 那么
那么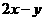 的最大值為
的最大值為
A.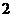 B.
B.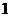 C.
C.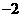 D.
D.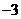
解:當直線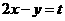 過點(0,-1)時,
過點(0,-1)時,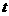 最大,故選B。
最大,故選B。
22.(湖南卷)對1個單位質量的含污物體進行清洗,清洗前其清潔度(含污物體的清潔度定義為: )為0.8,要求洗完后的清潔度是0.99.有兩種方案可供選擇,方案甲:一次清洗;方案乙:兩次清洗.該物體初次清洗后受殘留水等因素影響,其質量變為
)為0.8,要求洗完后的清潔度是0.99.有兩種方案可供選擇,方案甲:一次清洗;方案乙:兩次清洗.該物體初次清洗后受殘留水等因素影響,其質量變為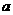 (1≤a≤3).設用
(1≤a≤3).設用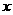 單位質量的水初次清洗后的清潔度是
單位質量的水初次清洗后的清潔度是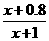 (
(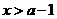 ),用
),用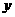 質量的水第二次清洗后的清潔度是
質量的水第二次清洗后的清潔度是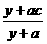 ,其中
,其中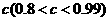 是該物體初次清洗后的清潔度.
是該物體初次清洗后的清潔度.
(Ⅰ)分別求出方案甲以及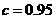 時方案乙的用水量,并比較哪一種方案用水量較少;
時方案乙的用水量,并比較哪一種方案用水量較少;
(Ⅱ)若采用方案乙,當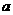 為某定值時,如何安排初次與第二次清洗的用水量,使總用水量最少?并討論
為某定值時,如何安排初次與第二次清洗的用水量,使總用水量最少?并討論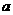 取不同數值時對最少總用水量多少的影響.
取不同數值時對最少總用水量多少的影響.
解:(Ⅰ)設方案甲與方案乙的用水量分別為x與z,由題設有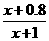 =0.99,解得x=19.
=0.99,解得x=19.
由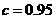 得方案乙初次用水量為3, 第二次用水量y滿足方程:
得方案乙初次用水量為3, 第二次用水量y滿足方程:
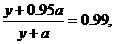 解得y=4
解得y=4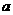 ,故z=4
,故z=4 +3.即兩種方案的用水量分別為19與4
+3.即兩種方案的用水量分別為19與4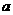 +3.
+3.
因為當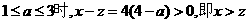 ,故方案乙的用水量較少.
,故方案乙的用水量較少.
(II)設初次與第二次清洗的用水量分別為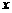 與
與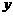 ,類似(I)得
,類似(I)得
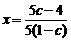 ,
,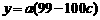 (*)
(*)
于是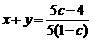 +
+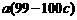
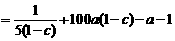
當 為定值時,
為定值時,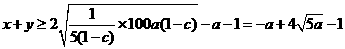 ,
,
當且僅當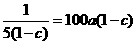 時等號成立.此時
時等號成立.此時

將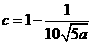 代入(*)式得
代入(*)式得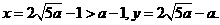
故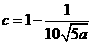 時總用水量最少, 此時第一次與第二次用水量分別為
時總用水量最少, 此時第一次與第二次用水量分別為 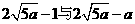 , 最少總用水量是
, 最少總用水量是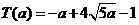 .
.
當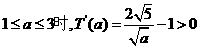 ,故T(
,故T(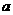 )是增函數(也可以用二次函數的單調性判斷).這說明,隨著
)是增函數(也可以用二次函數的單調性判斷).這說明,隨著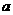 的值的最少總用水量, 最少總用水量最少總用水量.
的值的最少總用水量, 最少總用水量最少總用水量.
20.(上海春)不等式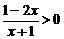 的解集是 .
的解集是 .
解:應用結論: 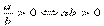 .不等式
.不等式 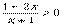 等價于(1-2x)(x+1)>0,也就是
等價于(1-2x)(x+1)>0,也就是 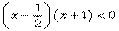 ,所以
,所以 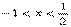 ,從而應填
,從而應填 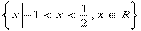 .
21.(上海春)已知直線
.
21.(上海春)已知直線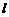 過點
過點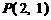 ,且與
,且與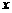 軸、
軸、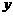 軸的正半軸分別交于
軸的正半軸分別交于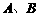 兩點,
兩點,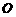 為坐標原點,則三角形
為坐標原點,則三角形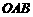 面積的最小值為 .
面積的最小值為 .
解:設直線 l 為 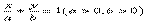 ,則有關系
,則有關系
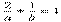 . 對
. 對 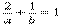 應用2元均值不等式,得
應用2元均值不等式,得
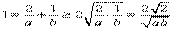 ,即ab≥8 .于是,△OAB 面積為
,即ab≥8 .于是,△OAB 面積為
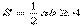 .從而應填4.
.從而應填4.
19.(浙江卷)不等式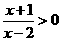 的解集是 。.
的解集是 。.
解: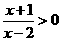 Û(x+1)(x-2)>0Ûx<-1或x>2.
Û(x+1)(x-2)>0Ûx<-1或x>2.
18.(天津卷)某公司一年購買某種貨物400噸,每次都購買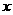 噸,運費為4萬元/次,一年的總存儲費用為
噸,運費為4萬元/次,一年的總存儲費用為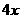 萬元,要使一年的總運費與總存儲費用之和最小,則
萬元,要使一年的總運費與總存儲費用之和最小,則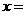 _______
噸.
_______
噸.
解:某公司一年購買某種貨物400噸,每次都購買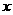 噸,則需要購買
噸,則需要購買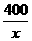 次,運費為4萬元/次,一年的總存儲費用為
次,運費為4萬元/次,一年的總存儲費用為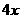 萬元,一年的總運費與總存儲費用之和為
萬元,一年的總運費與總存儲費用之和為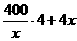 萬元,
萬元,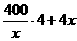 ≥160,當
≥160,當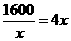 即
即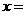 20噸時,一年的總運費與總存儲費用之和最小。
20噸時,一年的總運費與總存儲費用之和最小。
17.(上海卷)三個同學對問題“關于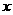 的不等式
的不等式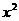 +25+|
+25+|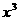 -5
-5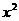 |≥
|≥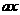 在[1,12]上恒成立,求實數
在[1,12]上恒成立,求實數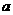 的取值范圍”提出各自的解題思路.
的取值范圍”提出各自的解題思路.
甲說:“只須不等式左邊的最小值不小于右邊的最大值”.
乙說:“把不等式變形為左邊含變量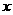 的函數,右邊僅含常數,求函數的最值”.
的函數,右邊僅含常數,求函數的最值”.
丙說:“把不等式兩邊看成關于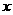 的函數,作出函數圖像”.
的函數,作出函數圖像”.
參考上述解題思路,你認為他們所討論的問題的正確結論,即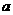 的取值范圍是 .
的取值范圍是 .
解:由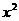 +25+|
+25+|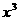 -5
-5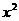 |≥
|≥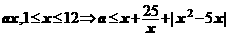 ,而
,而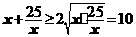 ,等號當且僅當
,等號當且僅當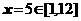 時成立;且
時成立;且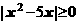 ,等號當且僅當
,等號當且僅當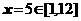 時成立;所以,
時成立;所以,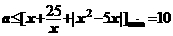 ,等號當且僅當
,等號當且僅當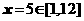 時成立;故
時成立;故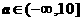 ;
;
16.(江蘇卷)不等式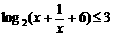 的解集為
的解集為
[思路點撥]本題考查對數函數單調性和不等式的解法
[正確解答]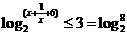 ,0〈
,0〈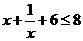 ,
,
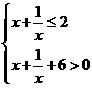 .
.
解得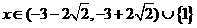
[解后反思]在數的比較大小過程中,要遵循這樣的規律,異中求同即先將這些數的部分因式化成相同的部分,再去比較它們剩余部分,就會很輕易啦.一般在數的比較大小中有如下幾種方法:(1)作差比較法和作商比較法,前者和零比較,后者和1比較大小;(2)找中間量,往往是1,在這些數中,有的比1大,有的比1小;,(3)計算所有數的值;(4)選用數形結合的方法,畫出相應的圖形;(5)利用函數的單調性等等.
15.(上海春)若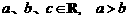 ,則下列不等式成立的是( )
,則下列不等式成立的是( )
(A)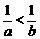 . (B)
. (B)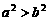 . (C)
. (C)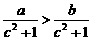 .(D)
.(D)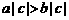 .
.
解:應用間接排除法.取a=1,b=0,排除A. 取a=0,b=-1,排除B; 取c=0,排除D.故應該選C.顯然 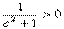 ,對不等式a>b的兩邊同時乘以
,對不等式a>b的兩邊同時乘以 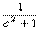 ,立得
,立得
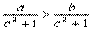 成立.
成立.
14.(重慶卷)若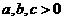 且
且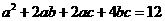 ,則
,則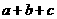 的最小值是
的最小值是
(A)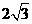 (B)3 (C)2 (D)
(B)3 (C)2 (D)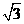
解:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=12+(b-c)2³12,當且僅當b=c時取等號,故選A
13.(重慶卷)若a,b,c>0且a(a+b+c)+bc=4-2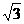 ,則2a+b+c的最小值為
,則2a+b+c的最小值為
(A)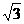 -1 (B)
-1 (B) 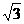 +1
(C) 2
+1
(C) 2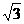 +2
(D) 2
+2
(D) 2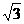 -2
-2
解析:若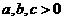 且
且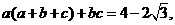 所以
所以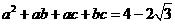 ,
,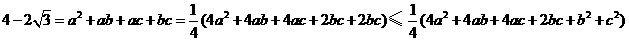 ∴
∴ 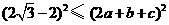 ,則(
,則(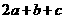 )≥
)≥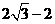 ,選D.
,選D.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com