
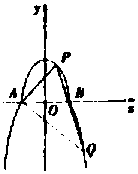
 如圖,曲線C由上半橢圓${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分拋物線${C_2}:y=-{x^2}+1(y≤0)$連接而成,C1與C2的公共點為A,B,其中C1的離心率為$\frac{{\sqrt{3}}}{2}$.
如圖,曲線C由上半橢圓${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分拋物線${C_2}:y=-{x^2}+1(y≤0)$連接而成,C1與C2的公共點為A,B,其中C1的離心率為$\frac{{\sqrt{3}}}{2}$.分析 (1)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半橢圓C1的左右頂點,設C1的半焦距為c,由$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$及a2-c2=b2-1,聯立解得a.
(2)由(1),上半橢圓C1的方程為$\frac{y^2}{4}+{x^2}=1(y≥0)$,由題意知,直線l與x軸不重合也不垂直,設其方程為
y=k(x-1)(k≠0),代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0,設點P的坐標為(xP,yP),由求根公式,得點P的坐標為$(\frac{{{k^2}-4}}{{{k^2}+4}},\frac{-8k}{{{k^2}+4}})$,同理,由$\left\{\begin{array}{l}{y=k(x-1),k≠0}\\{y=-{x}^{2}+1,y≤0}\end{array}\right.$,得點Q的坐標為(-k-1,-k2-2k),依題意可知AP⊥AQ,所以$\overrightarrow{A{P_1}}•\overrightarrow{AQ}=0$,即可得出k.
解答 解:(1)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半橢圓C1的左右頂點,
設C1的半焦距為c,由$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$及a2-c2=b2-1,
可得a=2,所以a=2,b=1.
(2)由(1),上半橢圓C1的方程為$\frac{y^2}{4}+{x^2}=1(y≥0)$,
由題意知,直線l與x軸不重合也不垂直,設其方程為y=k(x-1)(k≠0),
代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0,
設點P的坐標為(xP,yP),
因為直線l過點B,所以x=1是方程的一個根,
由求根公式,得${x_P}=\frac{{{k^2}-4}}{{{k^2}+4}},{y_P}=\frac{-8k}{{{k^2}+4}}$,所以點P的坐標為$(\frac{{{k^2}-4}}{{{k^2}+4}},\frac{-8k}{{{k^2}+4}})$,
同理,由$\left\{\begin{array}{l}{y=k(x-1),k≠0}\\{y=-{x}^{2}+1,y≤0}\end{array}\right.$,得點Q的坐標為(-k-1,-k2-2k),
所以$\overrightarrow{AP}=(\frac{{2{k^2}}}{{{k^2}+4}},\frac{{-8{k^2}}}{{{k^2}+4}}),\overrightarrow{AQ}=(-k,-{k^2}+2k)$,
依題意可知AP⊥AQ,所以$\overrightarrow{A{P_1}}•\overrightarrow{AQ}=0$,即$\frac{{2{k^2}}}{{{k^2}+4}}•(-k)+\frac{{-8{k^2}}}{{{k^2}+4}}•(-{k^2}-2k)=0$,
即$\frac{{-2{k^2}}}{{{k^2}+4}}[k-4(k+2)]=0$,
因為k≠0,所以k-4(k+2)=0,解得$k=-\frac{8}{3}$,
經檢驗,$k=-\frac{8}{3}$符合題意,故直線l的方程為$y=-\frac{8}{3}(x-1)$.
點評 本題考查了直線與橢圓拋物線相交問題、一元二次方程的根與系數的關系、圓的性質、向量垂直與數量積的關系,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{5}{3}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | -5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
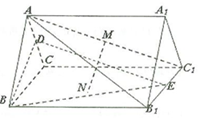 如圖,正三棱柱ABC-A1B1C1中,側棱$A{A_1}=\sqrt{3}$,AB=2,D,E分別為棱AC,B1C1的中點,M,N分別為線段AC1和BE的中點.
如圖,正三棱柱ABC-A1B1C1中,側棱$A{A_1}=\sqrt{3}$,AB=2,D,E分別為棱AC,B1C1的中點,M,N分別為線段AC1和BE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
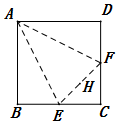 如圖,在正方形ABCD中,E,F分別為BC,CD的中點,H為EF的中點,沿AE,EF,FA將正方形折起,使B,C,D重合于點O,構成四面體,則在四面體A-OEF中,下列說法不正確的序號是②.
如圖,在正方形ABCD中,E,F分別為BC,CD的中點,H為EF的中點,沿AE,EF,FA將正方形折起,使B,C,D重合于點O,構成四面體,則在四面體A-OEF中,下列說法不正確的序號是②.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com