
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
分析 求函數f(x)的定義域,求出f′(x),利用導數和極值之間的關系將條件轉化:f′(x)=0在(0,+∞)上有根,即即2x2-ax+1=0在(0,+∞)上有根,根據二次方程根的分布問題列出方程組,根據條件列出關于a的不等式,求出a的范圍.
解答 解:f(x)=ax-x2-lnx,x∈(0,+∞),
則f′(x)=a-2x-$\frac{1}{x}$=-$\frac{2{x}^{2}-ax+1}{x}$,
∵函數f(x)存在極值,∴f′(x)=0在(0,+∞)上有根,
即2x2-ax+1=0在(0,+∞)上有根,∴△=a2-8≥0,
顯然當△=0時,F(x)無極值,不合題意;
∴方程必有兩個不等正根,記方程2x2-ax+1=0的兩根為x1,x2,x1+x2=$\frac{a}{2}$,x1x2=$\frac{1}{2}$,
f(x1),f(x2)是函數F(x)的兩個極值,
由題意得,f(x1)+f(x2)=a(x1+x2)-(x12+x22)-(lnx1+lnx2)
=$\frac{{a}^{2}}{2}$-$\frac{{a}^{2}}{4}$+1-ln$\frac{1}{2}$>5-ln$\frac{1}{2}$,
化簡解得,a2>16,滿足△>0,
又x1+x2=$\frac{a}{2}$>0,即a>0,
∴∴a的取值范圍是(4,+∞),
故選:B.
點評 本題考查導數與函數的單調性、極值的關系,以及二次方程根的分布問題,考查轉化思想,化簡、變形能力,綜合性大、難度大,屬于中檔題.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:解答題
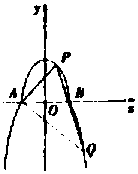 如圖,曲線C由上半橢圓${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分拋物線${C_2}:y=-{x^2}+1(y≤0)$連接而成,C1與C2的公共點為A,B,其中C1的離心率為$\frac{{\sqrt{3}}}{2}$.
如圖,曲線C由上半橢圓${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分拋物線${C_2}:y=-{x^2}+1(y≤0)$連接而成,C1與C2的公共點為A,B,其中C1的離心率為$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
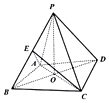 如圖,在四棱錐P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等邊三角形,E是BP中點,AC與BD交于點O,且OP⊥平面ABCD.
如圖,在四棱錐P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等邊三角形,E是BP中點,AC與BD交于點O,且OP⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com