Question

12．如圖，過點B（0，-b）作橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的弦，求這些弦中的最大弦長．

Answer 1

分析 設M（x，y）是橢圓上任一點，|BM|²=x²+（y+b）²=x²+y²+2by+b²，由x²=$\frac{{a}^{2}}{{b}^{2}}$（b²-y²），整理得|BM|²=（1-$\frac{{a}^{2}}{{b}^{2}}$）y²+2by+（a²+b²）=（1-$\frac{{a}^{2}}{{b}^{2}}$）•（y-$\frac{{b}^{3}}{{c}^{2}}$）²+$\frac{{a}^{4}}{{c}^{2}}$，分類當b≤c，即b≤$\frac{\sqrt{2}}{2}$a時，$\frac{{b}^{3}}{{c}^{2}}$≤b，y=$\frac{{b}^{3}}{{c}^{2}}$時，|BM|的最大值為$\frac{{a}^{2}}{c}$，同理可知：當b＞c，即y=b時，點M在（0，b），即y軸上之頂點位置，|BM|的最大值為2b．

解答 解：設M（x，y）是橢圓上任一點，
|BM|²=x²+（y+b）²=x²+y²+2by+b²，
由$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，
則x²=$\frac{{a}^{2}}{{b}^{2}}$（b²-y²），將其代入上式，整理得：|BM|²=（1-$\frac{{a}^{2}}{{b}^{2}}$）y²+2by+（a²+b²）
=（1-$\frac{{a}^{2}}{{b}^{2}}$）•（y-$\frac{{b}^{3}}{{c}^{2}}$）²+$\frac{{a}^{4}}{{c}^{2}}$．
∵-b≤y≤b，
（1）當b≤c，即b≤$\frac{\sqrt{2}}{2}$a時，$\frac{{b}^{3}}{{c}^{2}}$≤b，
∴y=$\frac{{b}^{3}}{{c}^{2}}$時，|BM|的最大值為$\frac{{a}^{2}}{c}$，
（2）當b＞c，即b＞$\frac{\sqrt{2}}{2}$a時，$\frac{{b}^{3}}{{c}^{2}}$＞b，
故y=b時，點M在（0，b），
即y軸上之頂點位置，|BM|²的最大值為（1-$\frac{{a}^{2}}{{b}^{2}}$）（b-$\frac{{b}^{3}}{{c}^{2}}$）²+$\frac{{a}^{4}}{{c}^{2}}$=4b²，
∴|BM|的最大值為2b．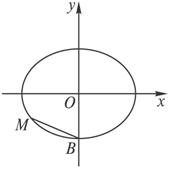

點評 本題考查橢圓的標準方程及性質，考查橢圓弦長公式的最值，考查二次函數的最值，考查計算能力，屬于中檔題．