
 已知函數f(x)=cos(x+$\frac{π}{6}$)+sinx.
已知函數f(x)=cos(x+$\frac{π}{6}$)+sinx.| x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{3}$ | $\frac{π}{6}$ | $\frac{2π}{3}$ | $\frac{7π}{6}$ | $\frac{5π}{3}$ |
| f(x) | 0 | 1 | 0 | -1 | 0 |
分析 (Ⅰ)利用三角函數恒等變換的應用化簡函數解析式可得f(x)=sin(x+$\frac{π}{3}$),利用“五點法”,即可列表并畫出函數的圖象.
(Ⅱ)由(Ⅰ)可得sin(A+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,結合范圍0<A<π,可求A,由正弦定理可求sinB=$\frac{1}{2}$,結合范圍0$<B<\frac{2π}{3}$,可求B,進而可求C,利用三角形面積公式即可計算得解.
解答 (本小題滿分12分)
解:(Ⅰ)f(x)=cos(x+$\frac{π}{6}$)+sinx
=cosxcos$\frac{π}{6}$-sinxsin$\frac{π}{6}$+sinx
=$\frac{\sqrt{3}}{2}$cosx+$\frac{1}{2}$sinx
=sin(x+$\frac{π}{3}$),…(2分)
利用“五點法”列表如下,
| x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{3}$ | $\frac{π}{6}$ | $\frac{2π}{3}$ | $\frac{7π}{6}$ | $\frac{5π}{3}$ |
| y | 0 | 1 | 0 | -1 | 0 |
 …(6分)
…(6分)點評 本題主要考查了三角函數恒等變換的應用,五點作圖法,考查了正弦定理,三角形面積公式在解三角形中的應用,屬于基礎題.


科目:高中數學 來源: 題型:解答題
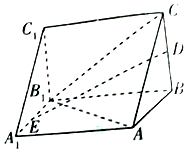 在如圖所示的三棱錐ABC-A1B1C1中,AA1⊥底面ABC,D,E分別是BC,A1B1的中點.
在如圖所示的三棱錐ABC-A1B1C1中,AA1⊥底面ABC,D,E分別是BC,A1B1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
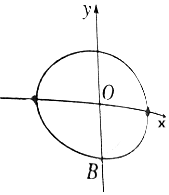
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{-\frac{1}{2},\frac{1}{2}}]$ | B. | $({-\frac{1}{2},\frac{1}{2}})$ | C. | [-1,1] | D. | (-1,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ∅ | B. | p9vv5xb5 | C. | {a,c} | D. | {b,e} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x1)>f(x2) | B. | f(x1)<f(x2) | ||
| C. | f(x1)=f(x2) | D. | 無法比較f(x1)與f(x2)的大小 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{1}{2}$,2] | B. | (-1,+∞) | C. | (-$\frac{1}{2}$,0)∪(0,2) | D. | (-$\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x+$\frac{1}{x}$ | B. | f(x)=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | D. | y=$\sqrt{x-1}$+$\frac{1}{\sqrt{x-1}}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com