
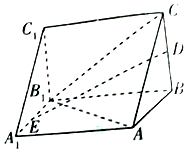
 在如圖所示的三棱錐ABC-A1B1C1中,AA1⊥底面ABC,D,E分別是BC,A1B1的中點.
在如圖所示的三棱錐ABC-A1B1C1中,AA1⊥底面ABC,D,E分別是BC,A1B1的中點.分析 (1)根據題目特點,可由證面面平行,得到線面平行.
(2)方法一:找出線面所成角,再構造三角形求線面角的正切值;方法二:建立空間直角坐標系,根據向量所成角,求得線面角.
解答 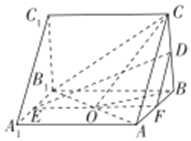 解:(1)取AB的中點F,連接DF,EF…(1分)
解:(1)取AB的中點F,連接DF,EF…(1分)
在△ABC中,因為D,F分別為BC,AB的中點,
所以DF∥AC(中位線),
又∵DF?平面ACC1A1,AC?平面ACC1A1,
所以DF∥平面ACC1A1…(3分)
在矩形ABB1A1中,因為E,F分別為A1B1,AB的中點,
∴EF∥AA1(中位線),
又∵EF?平面 ACC1A1,AA1?平面ACC1A1,
∴EF∥平面ACC1A1…(4分)
∵DF∩EF=F,
∴平面DEF∥平面ACC1A1…(5分)
∵DE?平面DEF,
∴DE∥平面ACC1A1…(6分)
(2)解法一:
∵三棱柱ABC-A1B1C1為直三棱柱,
∴BC⊥BB1,
又AB⊥BC,AB∩BB1=B,
∴BC⊥平面ABB1A1,…(7分)
∵AB=BC,BB1=BB1,
∴△ABB1≌△CBB1
∴AB1=CB1,又$∠AC{B_1}={60^0}$,
∴△AB1C為正三角形,
∴$A{B_1}=\sqrt{A{B^2}+BB_1^2}=AC=\sqrt{2}AB$,∴BB1=AB…(8分)
取AB1的中點O,連接BO,CO,
∴AB1⊥BO,AB1⊥CO,
∴AB1⊥平面BCO,
∴平面AB1C⊥平面BCO,點B在平面AB1C上的射影在CO上,
∴∠BCO即為直線BC與平面AB1C所成角…(10分)
在Rt△BCO中,$BO=\frac{{\sqrt{2}}}{2}AB=\frac{{\sqrt{2}}}{2}BC$,
∴$tan∠BCO=\frac{BO}{BC}=\frac{{\sqrt{2}}}{2}$…(12分)
解法二:由題知 BB1,BA,BC兩兩互相垂直,故建立空間直角坐標線如圖,
BB1,BA,BC兩兩互相垂直,故建立空間直角坐標線如圖,
并設AB=2,BB1=t,
則A(0,2,0),C(0,0,2),B1(t,0,0)(t>0)
∴$\overrightarrow{CA}=(0,2,-2)$,$\overrightarrow{C{B}_{1}}=(t,0,-2)$
∵$∠AC{B_1}={60^0}$,∴$<\overrightarrow{CA},\overrightarrow{C{B}_{1}}>$=60°
∴$cos60°=\frac{4}{2\sqrt{2}\sqrt{{t}^{2}+4}}$,得t=2.
∴B1(2,0,0),$\overrightarrow{C{B}_{1}}=(2,0,-2)$,
設平面AB1C的法向量為$\overrightarrow{n}=(x,y,z)$
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CA}=0}\\{\overrightarrow{n}•\overrightarrow{C{B}_{1}}=0}\end{array}\right.$ 得x=y=z,取$\overrightarrow{n}$=(1,1,1)
記直線BC與平面AB1C所成角為θ,且$\overrightarrow{BC}=(0,0,2)$
則$sinθ=\frac{|\overrightarrow{n}•\overrightarrow{BC}|}{|\overrightarrow{n}||\overrightarrow{BC}|}$=$\frac{2}{\sqrt{3}×2}=\frac{\sqrt{3}}{3}$
∴$tanθ=\frac{\sqrt{2}}{2}$
故直線BC與平面AB1C所成角的正切值為$\frac{\sqrt{2}}{2}$.
點評 考查線面、面面位置關系的判斷與證明,直線與平面所成角的求法.屬于中檔題.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|x>0} | B. | {x|x<-3} | C. | {x|-3<x≤-1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
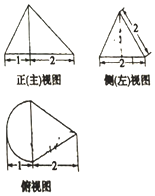
| A. | $\frac{{(4+π)\sqrt{3}}}{3}$ | B. | $\frac{(4+π)\sqrt{3}}{2}$ | C. | $\frac{(4+π)\sqrt{3}}{6}$ | D. | (4+π)$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{-4ln4,-\frac{4}{e}}]$ | B. | [-4ln4,-ln4] | C. | $[{-\frac{4}{e},-ln4}]$ | D. | $({-\frac{4}{e},-ln4}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a=30,b=40,A=30° | B. | a=25,b=30,A=150° | ||
| C. | a=8,b=16,A=30° | D. | a=72,b=60,A=135° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=cos(x+$\frac{π}{6}$)+sinx.
已知函數f(x)=cos(x+$\frac{π}{6}$)+sinx.| x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{3}$ | $\frac{π}{6}$ | $\frac{2π}{3}$ | $\frac{7π}{6}$ | $\frac{5π}{3}$ |
| f(x) | 0 | 1 | 0 | -1 | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com