
分析 證法一:設0<x1<x2,作差判斷f(x1)與f(x2)的大小,根據函數單調性的定義,可得f(x)=-x2+3在(0,+∞)上是減函數.
證法二:求導,根據當x∈(0,+∞)時,f′(x)<0恒成立,可得:f(x)=-x2+3在(0,+∞)上是增函數
解答 證法一:設0<x1<x2…(2分)
則$f({x_1})-f({x_2})=-x_1^2+3-({-x_2^2+3})$…(4分)
=$x_2^2-x_1^2=({{x_2}+{x_1}})({{x_2}-{x_1}})$…(6分)
∵0<x1<x2,
∴x2+x1>0,x2-x1>0,
∴f(x1)-f(x2)>0
∴f(x1)>f(x2),
∴f(x)=-x2+3在(0,+∞)上是增函數…(10分)
證法二:∵f(x)=-x2+3,
∴f′(x)=-2x,…(4分)
當x∈(0,+∞)時,
f′(x)<0恒成立,…(8分)
∴f(x)=-x2+3在(0,+∞)上是增函數…(10分)
點評 本題考查的知識點是利用導數研究函數的單調性,難度中檔.


科目:高中數學 來源: 題型:選擇題
| A. | x-2y-7=0 | B. | 2x+y+1=0 | C. | x-2y+7=0 | D. | 2x+y-1=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<-2,或a>7 | B. | -2<a<7 | C. | -7<a<2 | D. | a=-2,或a=7 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 設U=R,集合A={x|-2<x<1},B={x|-1<x≤4},則如圖中陰影部分表示的集合為{x|x≤-2,或-1<x<1,或x>4}.
設U=R,集合A={x|-2<x<1},B={x|-1<x≤4},則如圖中陰影部分表示的集合為{x|x≤-2,或-1<x<1,或x>4}.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1,+∞] | B. | (-1,0] | C. | (-1,+∞) | D. | (-1,0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x+1 | B. | x-1 | C. | x-2 | D. | x-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
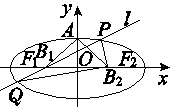 如圖,設橢圓的中心為原點O,長軸在x軸上,上頂點為A,左、右焦點分別為F1,F2,線段OF1,OF2的中點分別為B1,B2,且△AB1B2是面積為4的直角三角形.過B1作l交橢圓于P、Q兩點,使PB2垂直QB2,求直線l的方程x+2y+2=0和x-2y+2=0.
如圖,設橢圓的中心為原點O,長軸在x軸上,上頂點為A,左、右焦點分別為F1,F2,線段OF1,OF2的中點分別為B1,B2,且△AB1B2是面積為4的直角三角形.過B1作l交橢圓于P、Q兩點,使PB2垂直QB2,求直線l的方程x+2y+2=0和x-2y+2=0.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com