
| A. | x+1 | B. | x-1 | C. | x-2 | D. | x-$\frac{3}{2}$ |
分析 根據${∫}_{0}^{1}$g(t)dt是常數值,得出g(x)是一次函數,利用待定系數法即可求出g(x)的解析式.
解答 解:∵g(x)=x-${∫}_{0}^{1}$g(t)dt-$\frac{3}{2}$,
∵${∫}_{0}^{1}$g(t)dt為常數,
∴g(x)為一次函數,
設g(x)=ax+b,
${∫}_{0}^{1}$g(x)dx=($\frac{1}{2}$ax2+bx)|${\;}_{0}^{1}$=$\frac{1}{2}$a+b,
∴g(x)=x-${∫}_{0}^{1}$g(t)dt-$\frac{3}{2}$=x-($\frac{1}{2}$a+b)-$\frac{3}{2}$=ax+b,
∴a=1,b=-1,
∴g(x)=x-1,
故選:B
點評 本題考查了利用待定系數法求函數解析式的應用問題,也考查了定積分簡單應用問題,是綜合性題目.


 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | 如果m?α,n?α,m、n是異面直線,那么n∥α | |
| B. | 如果m?α,n與α相交,那么m、n是異面直線 | |
| C. | 如果m?α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m∥α,n∥α,m、n共面,那么m∥n |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0<a≤$\frac{1}{3}$ | B. | a≤$\frac{1}{3}$ | C. | $\frac{1}{3}$≤a<1 | D. | a≥3或0<a<1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $4\sqrt{5}$ | D. | $-4\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
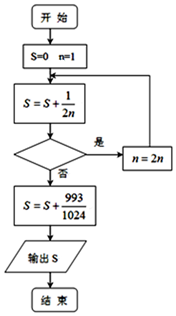
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com