
分析 利用誘導公式和二倍角公式化簡得y=$\frac{1}{2}$cos2x,周期T=π,則相鄰兩個對稱中心的距離為$\frac{π}{2}$,故①錯誤;根據否命題的定義可知②錯誤;“a+b=0”是“a=5,且b=-5”的必要不充分條件,而原命題與逆否命題真假性相同,故③正確;根據命題的否定的定義可知④正確;利用對數函數的單調性即可判斷⑤正確;當$\overrightarrow{a}•\overrightarrow{b}<$0時,$|\overrightarrow{a}-\overrightarrow{b}|>|\overrightarrow{a}+\overrightarrow{b}|$,故⑥錯誤;根據向量的數量積定義可知⑦正確.
解答 解:對于①:y=cos(x-$\frac{π}{4}$)cos(x+$\frac{π}{4}$)=cos[$(x+\frac{π}{4})-\frac{π}{2}$]cos(x+$\frac{π}{4}$)=sin(x+$\frac{π}{4}$)cos(x+$\frac{π}{4}$)=$\frac{1}{2}sin(2x+\frac{π}{2})=\frac{1}{2}cos2x$,周期T=π,所以相鄰兩個對稱中心的距離為$\frac{π}{2}$,故①錯誤;
對于②:根據否命題的定義可知,否命題是“若a≠0,則ab≠0”,故②錯誤;
對于③:因為“a=5,且b=-5”是“a+b=0”的充分不必要條件,所以“a+b=0”是“a=5,且b=-5”的必要不充分條件,根據原命題與逆否命題真假性相同的規律可知,“a≠5且b≠-5”是“a+b≠0”的必要不充分條件,故③正確;
對于④:根據命題的否定的定義可知,全稱命題的否定是特稱命題,故④正確;
對于⑤:因為0<a<1,所以y=logax在(0,+∞)上單調遞減,又因為a+1<1+$\frac{1}{a}$,所以$lo{g}_{a}(a+1)>lo{g}_{a}(1+\frac{1}{a})$,故⑤正確;
對于⑥:當$\overrightarrow{a}•\overrightarrow{b}<$0時,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}>{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$,所以$(\overrightarrow{a}-\overrightarrow{b})^{2}>(\overrightarrow{a}+\overrightarrow{b})^{2}$,即$|\overrightarrow{a}-\overrightarrow{b}|>|\overrightarrow{a}+\overrightarrow{b}|$,故⑥錯誤;
對于⑦:根據向量的數量積定義可知,⑦正確.
故答案為:③④⑤⑦
點評 本題通過判斷命題的真假考查了三角函數的圖象及性質,簡易邏輯,對數函數以及向量的有關知識,只有扎實掌握各章節基礎知識才能正確解答.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | x+1 | B. | x-1 | C. | x-2 | D. | x-$\frac{3}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
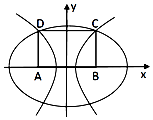 在平面直角坐標系xOy中,矩形ABCD的一邊AB在x軸上,另一邊CD在x軸上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).
在平面直角坐標系xOy中,矩形ABCD的一邊AB在x軸上,另一邊CD在x軸上方,且AB=8,BC=6,其中A(-4,0)、B(4,0).查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com