
分析 畫出函數f(x)=$\left\{\begin{array}{l}{1{0}^{-x}-2,x≤0}\\{2ax-1,x>0}\end{array}\right.$(a是常數且a>0)的圖象,
①由圖只需說明在點x=0處函數f(x)的最小值是-1;判斷①的正誤;
②利用函數的零點個數判斷②的正誤;
③只需說明f(x)>0在[$\frac{1}{2}$,+∞)上恒成立,則當x=$\frac{1}{2}$時,函數取得最小值,
從而求得a的取值范圍是a>1;判斷③的正誤;
④已知函數f(x)的圖象在(-∞,0))上是下凹的,所以任取兩點連線應在圖象的上方.判斷④的正誤;
解答  解:對于①,由圖只需說明在點x=0處函數f(x)的最小值是-1;故正確;
解:對于①,由圖只需說明在點x=0處函數f(x)的最小值是-1;故正確;
對于②,方程m=|f(x+k)|(k∈R)有兩個零點,而函數y=|f(x+k)|,由f(x)圖象左右平移后,x軸下方的部分對稱到x軸上方,m=1時,有3個零點,所以②不正確;
對于③,只需說明f(x)>0在[$\frac{1}{2}$,+∞)上恒成立,則當x=$\frac{1}{2}$時,函數取得最小值,求得a的取值范圍是a>1;不正確;
對于④,已知函數f(x)在(-∞,0)上的圖象是下凹的,所以任取兩點連線應在圖象的上方,即有f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$,故正確.
故答案為:①④.
點評 利用函數的圖象研究函數的單調區間,以及根據函數的增減性得到函數的最值是常用的方法,解答本題的關鍵是圖象法.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
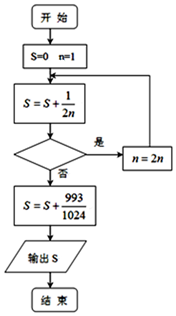
| A. | n<10 | B. | n≤10 | C. | n≤1024 | D. | n<1024 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=(x+1)2,x∈(0,+∞) | B. | y=log${\;}_{\frac{1}{2}}$x,x∈(1,+∞) | ||
| C. | y=2x-1 | D. | y=$\sqrt{2x-1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-3] | B. | (-∞,-3) | C. | [43,+∞) | D. | (-3,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com