
分析 求出f(x)的導數,可得切線的斜率,設g(x)=(3-x)ex-2,求出導數和單調區間,可得極值也為最值,假設存在m滿足題意,由直線方程可得斜率大于最值,即可判斷不存在.
解答 解:函數f(x)=(4-x)ex-2,
導數為f′(x)=(3-x)ex-2,
設g(x)=(3-x)ex-2,則g'(x)=(2-x)ex-2,
由x>2時,g'(x)<0,g(x)遞減;x<2時,g'(x)>0,g(x)遞增.
可推得g(x)極大值為g(2)=1,也為最大值.
假設y=f(x)與直線3x-2y+m=0(m為確定的常數)相切,
則切線的斜率為$\frac{3}{2}$,
由于切線的斜率的最大值為1.
所以$f'(x)=(3-x){e^{x-2}}=\frac{3}{2}$無解.
所以不存在m滿足題意.
點評 本題考查導數的運用:求切線的斜率和單調區間、極值和最值,考查存在性問題的解法,以及化簡整理的運算能力,屬于中檔題.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | 與a有關,且與b有關 | B. | 與a有關,但與b無關 | ||
| C. | 與a無關,且與b無關 | D. | 與a無關,但與b有關 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
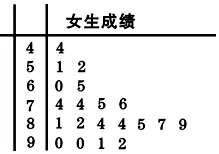 為了研究某學科成績(滿分100分)是否與學生性別有關,采用分層抽樣的方法,從高二年級抽取了30名男生和20名女生的該學科成績,得到如圖所示女生成績的莖葉圖.其中抽取的男生中有21人的成績在80分以下,規定80分以上為優秀(含80分).
為了研究某學科成績(滿分100分)是否與學生性別有關,采用分層抽樣的方法,從高二年級抽取了30名男生和20名女生的該學科成績,得到如圖所示女生成績的莖葉圖.其中抽取的男生中有21人的成績在80分以下,規定80分以上為優秀(含80分).| 優秀 | 非優秀 | 總計 | |
| 男生 | |||
| 女生 | |||
| 總計 | 50 |
| 參考數據 | 當x2≤2.706時,無充分證據判定變量A,B有關聯,可以認為兩變量無關聯; |
| 當x2>2.706時,有90%的把握判定變量A,B有關聯; | |
| 當x2>3.841時,有95%的把握判定變量A,B有關聯; | |
| 當x2>6.635時,有99%的把握判定變量A,B有關聯. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com