
| A. | 與a有關,且與b有關 | B. | 與a有關,但與b無關 | ||
| C. | 與a無關,且與b無關 | D. | 與a無關,但與b有關 |
分析 結合二次函數的圖象和性質,分類討論不同情況下M-m的取值與a,b的關系,綜合可得答案.
解答 解:函數f(x)=x2+ax+b的圖象是開口朝上且以直線x=-$\frac{a}{2}$為對稱軸的拋物線,
①當-$\frac{a}{2}$>1或-$\frac{a}{2}$<0,即a<-2,或a>0時,
函數f(x)在區間[0,1]上單調,
此時M-m=|f(1)-f(0)|=|a+1|,
故M-m的值與a有關,與b無關
②當$\frac{1}{2}$≤-$\frac{a}{2}$≤1,即-2≤a≤-1時,
函數f(x)在區間[0,-$\frac{a}{2}$]上遞減,在[-$\frac{a}{2}$,1]上遞增,
且f(0)>f(1),
此時M-m=f(0)-f(-$\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,
故M-m的值與a有關,與b無關
③當0≤-$\frac{a}{2}$<$\frac{1}{2}$,即-1<a≤0時,
函數f(x)在區間[0,-$\frac{a}{2}$]上遞減,在[-$\frac{a}{2}$,1]上遞增,
且f(0)<f(1),
此時M-m=f(1)-f(-$\frac{a}{2}$)=1+a+$\frac{{a}^{2}}{4}$,
故M-m的值與a有關,與b無關
綜上可得:M-m的值與a有關,與b無關
故選:B
點評 本題考查的知識點是二次函數的圖象和性質,熟練掌握二次函數的圖象和性質,是解答的關鍵.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖所示的莖葉圖記錄了甲、乙兩組各5名工人某日的產量數據(單位:件).若這兩組數據的中位數相等,且平均值也相等,則x和y的值分別為( )
如圖所示的莖葉圖記錄了甲、乙兩組各5名工人某日的產量數據(單位:件).若這兩組數據的中位數相等,且平均值也相等,則x和y的值分別為( )| A. | 3,5 | B. | 5,5 | C. | 3,7 | D. | 5,7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)在(0,2)單調遞增 | B. | f(x)在(0,2)單調遞減 | ||
| C. | y=f(x)的圖象關于直線x=1對稱 | D. | y=f(x)的圖象關于點(1,0)對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
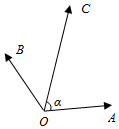 如圖,在同一個平面內,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分別為1,1,$\sqrt{2}$,$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為α,且tanα=7,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),則m+n=3.
如圖,在同一個平面內,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分別為1,1,$\sqrt{2}$,$\overrightarrow{OA}$與$\overrightarrow{OC}$的夾角為α,且tanα=7,$\overrightarrow{OB}$與$\overrightarrow{OC}$的夾角為45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),則m+n=3.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com