
分析 (Ⅰ)求f(x)在區間[0,π]內的單調區間;
(Ⅱ)利用同角三角函數基本關系式以及兩角和與差的三角函數化簡求解即可.
解答 解:(Ⅰ)函數f(x)=cos$\frac{x}{2}$sin($\frac{x}{2}$+$\frac{π}{3}$)-$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{\sqrt{3}}{4}$
=cos$\frac{x}{2}$($\frac{1}{2}$sin$\frac{x}{2}$+$\frac{\sqrt{3}}{2}$cos$\frac{x}{2}$)-$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sinx-$\frac{\sqrt{3}}{2}•\frac{1+cosx}{2}+\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sin(x-$\frac{π}{3}$).
x∈[0,π],x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
令t=x-$\frac{π}{3}$,y=sint在[-$\frac{π}{3}$,$\frac{π}{2}$]內的單調增函數;
y=sint在$[\frac{π}{2},\frac{2π}{3}]$上單調減函數,
∴f(x)的單調增區間是[0,$\frac{5π}{6}$],單調減區間是[$\frac{5π}{6}$,π].
(Ⅱ)f(x0)=$\frac{2}{5}$,x0∈[0,$\frac{π}{2}$],f(x0)=$\frac{1}{2}$sin(x0-$\frac{π}{3}$)=$\frac{2}{5}$,
可得sin(x0-$\frac{π}{3}$)=$\frac{4}{5}$,cos(x0-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}({x}_{0}-\frac{π}{3})}$=$\frac{3}{5}$,
sinx0=sin[(x0-$\frac{π}{3}$)+$\frac{π}{3}$]=$\frac{1}{2}$×$\frac{4}{5}$$+\frac{\sqrt{3}}{2}×\frac{3}{5}$=$\frac{4+3\sqrt{3}}{10}$.
點評 本題考查三角函數的化簡求值,兩角和與差的三角函數,正弦函數的單調區間的求法,考查計算能力.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{29}{2}$ | B. | 2$\sqrt{60}$ | C. | $\frac{29}{4}$ | D. | $\frac{102}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
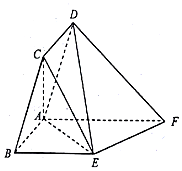 如圖,在平行四邊形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.
如圖,在平行四邊形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{7}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 與a有關,且與b有關 | B. | 與a有關,但與b無關 | ||
| C. | 與a無關,且與b無關 | D. | 與a無關,但與b有關 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com