
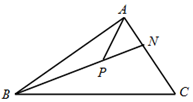
 如圖,在銳角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是線段BN(不含端點)上的一點,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,則$\frac{1}{m}$+$\frac{3}{n}$的最小值為16.
如圖,在銳角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是線段BN(不含端點)上的一點,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,則$\frac{1}{m}$+$\frac{3}{n}$的最小值為16. 分析 設$\overrightarrow{BP}$=t$\overrightarrow{BN}$,0<t<1,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示出$\overrightarrow{AP}$,求出m、n的表達式,再代入$\frac{1}{m}$+$\frac{3}{n}$求出它的最小值.
解答 解:設$\overrightarrow{BP}$=t$\overrightarrow{BN}$,0<t<1,
又$\overrightarrow{BN}$=$\overrightarrow{AN}$-$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$
=$\overrightarrow{AB}$+t$\overrightarrow{BN}$
=$\overrightarrow{AB}$+t($\overrightarrow{AN}$-$\overrightarrow{AB}$)
=(1-t)$\overrightarrow{AB}$+t$\overrightarrow{AN}$
=(1-t)$\overrightarrow{AB}$+$\frac{t}{3}$$\overrightarrow{AC}$,
∵$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,
∴m=1-t,n=$\frac{t}{3}$;
∴$\frac{1}{m}$+$\frac{3}{n}$=$\frac{1}{1-t}$+$\frac{9}{t}$
=($\frac{1}{1-t}$+$\frac{9}{t}$)(1-t+t)
=1+$\frac{t}{1-t}$+$\frac{9(1-t)}{t}$+9
≥2$\sqrt{\frac{t}{1-t}•\frac{9(1-t)}{t}}$+10
=2×3+10
=16,當且僅當t=$\frac{3}{4}$時“=”成立;
∴$\frac{1}{m}$+$\frac{3}{n}$的最小值是16.
故答案為:16.
點評 本題考查了平面向量的共線定理以及基本不等式的應用問題,是綜合性題目.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}+\sqrt{7}}{2}$ | B. | $\frac{\sqrt{11}+\sqrt{33}}{2}$ | C. | $\frac{\sqrt{3}+\sqrt{39}}{6}$ | D. | $\frac{1+\sqrt{17}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1] | B. | (1,2) | C. | [1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com