
分析 (I)求導數,據題意k=f′(1)=0,解得a值,再在定義域內解不等式f′(x)>0,f′(x)<0即可;
(II)f(x)的最大值大于1-$\frac{2}{a^2}$等價于lna2+a2<1,構造函數可判斷a的取值范圍;
解答 解:由已知有$f'(x)=\frac{1}{{{a^2}•x}}-1=\frac{{1-{a^2}•x}}{{{a^2}•x}}(x>0)$;
( I)因為f'(1)=0所以a2=1,即$f'(x)=\frac{1-x}{x}=0$得x=1;
因此函數f(x)的單調增區間為(0,1),單調減區間為(1,+∞).
( II)令f'(x)=0得$x=\frac{1}{a^2}({a^2}≠0)$,
則函數f(x)的在區間$(0,\frac{1}{a^2})$單調遞增,在區間$(\frac{1}{a^2},+∞)$.單調遞減;
即f(x)在$x=\frac{1}{a^2}$處取得最大值,最大值為$f(\frac{1}{a^2})=\frac{1}{a^2}ln\frac{1}{a^2}-\frac{1}{a^2}$;
因此f(x)的最大值大于1-$\frac{2}{a^2}$等價于lna2+a2<1…(*);
令t=a2(t>0),構造函數g(t)=lnt+t,則(*)式等價于g(t)=lnt+t<1;
因為函數g(t)=lnt+t在(0,+∞)為增函數且g(1)=1,
所以當0<t<1時有g(t)<1,當t>1時有g(t)>1;
即lna2+a2<1…(*)等價于0<a2<1即-1<a<0或0<a<1;
因此當f(x)的最大值大于1-$\frac{2}{a^2}$時,a的取值范圍(-1,0)∪(0,1).
點評 本題考查利用導數研究函數單調性、曲線上某點切線方程,考查函數的最值求解,考查分類討論思想,考查函數恒成立問題的解決,轉化函數最值是解決恒成立問題的常用方法.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
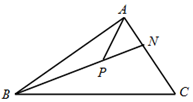 如圖,在銳角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是線段BN(不含端點)上的一點,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,則$\frac{1}{m}$+$\frac{3}{n}$的最小值為16.
如圖,在銳角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是線段BN(不含端點)上的一點,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,則$\frac{1}{m}$+$\frac{3}{n}$的最小值為16.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分接近π的實數的全體 | B. | 善良的人 | ||
| C. | A校高一(1)班所有聰明的學生 | D. | B單位所有身高在1.75 cm以上的人 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=x3+x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com